
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
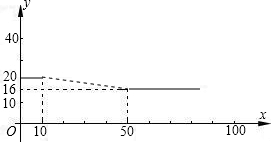 某种玩具专卖店,玩具每只进价12元,每只售价y元与购买只数x(只)之间的函数图象如图所示.
某种玩具专卖店,玩具每只进价12元,每只售价y元与购买只数x(只)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年湖北省九年级五月月考数学卷 题型:解答题
(本题满分10分)某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当售价的范围是是多少时,使得每件商品的利润率不超过80%且每个月的利润不低于2250元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com