
 的图像经过第一、三、四象限,则
的图像经过第一、三、四象限,则 的值可以是( )
的值可以是( ) .
. ;
;  .0;
.0;  .1;
.1;  .2.
.2.科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与
的图象与 轴、
轴、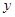 轴交于
轴交于 、
、 两点。
两点。
 、点
、点 的坐标和△
的坐标和△ 的面积。
的面积。 的长。
的长。 交于点
交于点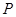 (
(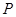 为一动点),把△
为一动点),把△ 的面积分成2︰1两部分,求直线L的解析式。
的面积分成2︰1两部分,求直线L的解析式。 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 配件种类 | 甲 | 乙 | 丙 |
| 每人每天可加工配件的数量 | 16 | 12 | 10 |
| 每个配件获利(元) | 6 | 8 | 5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:| |  型利润 型利润 |  型利润 型利润 |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两地相距120千米,甲乘坐一橡皮筏从
两地相距120千米,甲乘坐一橡皮筏从 地顺流去
地顺流去 地,2小时后,乙坐船从
地,2小时后,乙坐船从 地出发去
地出发去 地.如图为甲、乙两人离
地.如图为甲、乙两人离 地的路程
地的路程 (千米)与乙行进的时间
(千米)与乙行进的时间 (小时)的函数图象.乙到达
(小时)的函数图象.乙到达 地后,立即坐船返回.
地后,立即坐船返回. 地的距离.
地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com