练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．将一副三角板（△BAC和△ADE）如图放置，若AE∥BC，则∠CAE=30度，∠AFD=75度．

    分析 根据两直线平行，内错角相等可得∠CAE=∠C，再根据三角形的内角和定理求出∠AFE，然后根据平角的定义列式计算即可求出∠AFD．

    解答 解：∵AE∥BC，
    ∴∠CAE=∠C=30°，
    在△AEF中，∠AFE=180°∠CAE-∠E=180°-30°-45°=105°，
    ∴∠AFD=180°-∠AFE=180°-105°=75°．
    故答案为：30，75．

    点评 本题考查了平行线的性质，三角板的知识，熟记性质并准确识图，理清图中各角之间的关系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．已知二次函数y=2x2+4x-6．
    （1）将其化成y=a（x-h）2+k的形式；
    （2）写出图象的开口方向、对称轴、顶点坐标；
    （3）求图象与两坐标轴的交点坐标；
    （4）画出函数图象；
    （5）说明其图象与抛物线y=2x2的关系；
    （6）当x取何值时，函数y由最值？其最值是多少？
    （7）求函数图象与两坐标轴的交点所组成的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．小明从一定高度随机掷一枚质地均匀的硬币，他已经掷了两次硬币，结果都是“正面朝上”，那么，小明第三次掷硬币时，“反面朝上”的概率是（　　）
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．在平面直角坐标系xOy中，△ABC的位置如图所示．
    （1）分别写出△ABC各个顶点的坐标；
    （2）分别写出顶点A关于x轴对称的点A′的坐标和顶点B关于y轴对称的点B′的坐标；
    （3）求线段BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，水库中央有一建筑物AB，某人在地面D处测得其顶部A的仰角为30°，然后，自D处沿DB方向行50m至C，又测得其顶部A的仰角为60°，求建筑物AB的高．（结果精确到0.01m，$\sqrt{3}≈1.732$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知A、B两地相距100km，甲乙两人骑车同时分别从A，B两地相向而行．假设他们都保持匀速行驶．甲乙两人离A地的距离s（千米）与骑车时间t（小时）满足的函数关系图象如图所示．
    （1）请分别写出甲乙两人的s与t之间的函数表达式（不要求写自变量的取值范围）；
    （2）求1小时后，甲乙两人相距多少千米？
    （3）骑车多长时间后，甲乙两人相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

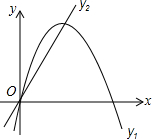    4．如图，已知抛物线y1=-x2+4x和直线y2=2x．我们约定：当x任取一值时，若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．下列判断：①当x＞2时，M=y2；②当x＜0时，x值越大，M值越大；③使得M大于4的x值不存在；④若M=2，则x=1．其中正确的说法有②③．（请填写正确说法的番号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

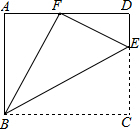    1．如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．
    （1）求证：△ABF∽△DFE；
    （2）若sin∠DFE=$\frac{1}{3}$，求tan∠EBC的值．
    （3）设$\frac{AB}{BC}$=k，是否存在k的值，使△ABF与△BFE相似？，若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算
    （1）-32-|（-5）3|×（-$\frac{2}{5}$）2-18÷|-（-3）2|；
    （2）-（-3）3×（-5）-（$\frac{1}{3}-\frac{1}{2}$）+（-$\frac{1}{6}$）

    查看答案和解析>>

    同步练习册答案