±2

,-8或5
分析:需要分类讨论:∠ACB=90°、∠ABC=90°和∠BAC=90°三种情况.利用两点间的距离公式和勾股定理来求t的值.
解答:
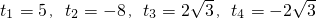
解:∵点A(2,m)和点B(-2,n)是反比例函数

图象上的两个点,
∴m=
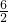
=3,n=
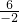
=-3,
∴A(2,3)、B(-2,-3).
①当∠ACB=90°时,在直角△ABC中,由勾股定理得到:AC
2+BC
2=AB
2,即
(2-t)
2+(3-1)
2+(-2-t)
2+(-3-1)
2=(-2-2)
2+(-3-3)
2,
解得,t
1=2

,t
2=-2

;
②当∠ABC=90°时,在直角△ABC中,由勾股定理得到:AB
2+BC
2=AC
2,即
(-2-2)
2+(-3-3)
2+(-2-t)
2+(-3-1)
2=(2-t)
2+(3-1)
2,
解得,t
3=-8;
③当∠BAC=90°时,在直角△ABC中,由勾股定理得到:AB
2+AC
2=BC
2,即
(-2-2)
2+(-3-3)
2+(2-t)
2+(3-1)
2=(-2-t)
2+(-3-1)
2,
解得,t
4=5;
综上所述,符合条件的t的值有:t
1=2

,t
2=-2

,t
3=-8,t
4=5;
故答案是:±2

,-8或5.
点评:本题考查了反比例函数综合题.解题时,要分类讨论,不要漏解.

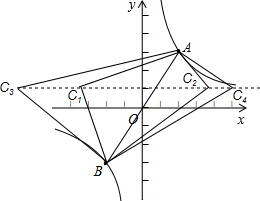
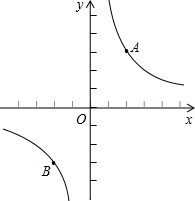 如图,点A(2,m)和点B(-2,n)是反比例函数
如图,点A(2,m)和点B(-2,n)是反比例函数 图象上的两个点,点C的坐标是(t,1),三角形ABC是直角三角形,则t的值是________.
图象上的两个点,点C的坐标是(t,1),三角形ABC是直角三角形,则t的值是________. ,-8或5
,-8或5
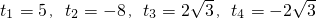
 图象上的两个点,
图象上的两个点,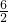 =3,n=
=3,n=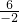 =-3,
=-3, ,t2=-2
,t2=-2 ;
; ,t2=-2
,t2=-2 ,t3=-8,t4=5;
,t3=-8,t4=5; ,-8或5.
,-8或5.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2