
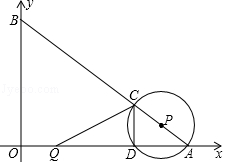
 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��8��0������0��6��������Q�ӵ�O������P�ӵ�Aͬʱ�������ֱ�����OA����AB�������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��5������PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�ΪC��D������CD��QC��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��B������ֱ�Ϊ��8��0������0��6��������Q�ӵ�O������P�ӵ�Aͬʱ�������ֱ�����OA����AB�������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��5������PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�ΪC��D������CD��QC������ ��1����ͼ1�У���PE��OA��E����PE��OB���Ƴ�$\frac{PA}{AB}$=$\frac{PE}{OB}$=$\frac{AE}{OA}$����$\frac{t}{10}$=$\frac{PE}{6}$=$\frac{AE}{8}$���Ƴ�PE=$\frac{3}{5}$t��AE=$\frac{4}{5}$t����PE��AD���Ƴ�DE=AE=$\frac{4}{5}$t���Ƴ�AD=$\frac{8}{5}$t��OQ=t���ɴ˰�t=$\frac{5}{2}$���뼴�ɽ�����⣮
��2�����P��Q��������꣬�����������빫ʽ���������κ������ö��κ��������ʼ��ɽ�����⣮
��3�����������η������ۢٵ�0��t��$\frac{40}{13}$ʱ���ڵ� $\frac{40}{13}$��t��5ʱ���ֱ���⼴�ɣ�
��� �⣺��1����ͼ1�У���PE��OA��E��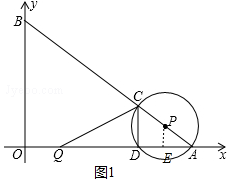
��A��8��0����B��0��6����
��OB=6��OA=8��AB=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��PE��OB��
��$\frac{PA}{AB}$=$\frac{PE}{OB}$=$\frac{AE}{OA}$��
��$\frac{t}{10}$=$\frac{PE}{6}$=$\frac{AE}{8}$��
��PE=$\frac{3}{5}$t��AE=$\frac{4}{5}$t��
��PE��AD��
��DE=AE=$\frac{4}{5}$t��
��AD=$\frac{8}{5}$t��
��t=$\frac{5}{2}$��
��AD=4��OQ=$\frac{5}{2}$��
��QD=8-$\frac{5}{2}$-4=$\frac{3}{2}$��
�ʴ�Ϊ4��$\frac{3}{2}$��
��2���ɣ�1����֪Q��t��0����P��8-$\frac{4}{5}$t��$\frac{3}{5}$t����
��PQ=$\sqrt{��t-8+\frac{4}{5}t��^{2}+��\frac{3}{5}t��^{2}}$=$\sqrt{\frac{90}{25}{t}^{2}-\frac{144}{5}t+64}$=$\sqrt{\frac{18}{5}��t-4��^{2}+\frac{32}{5}}$��
��$\frac{18}{5}$��0��
��t=4ʱ��PQ��ֵ��С����СֵΪ$\frac{4\sqrt{10}}{5}$��
��3����Rt��ACD�У�CD=AC•sin��BAO=2t��$\frac{3}{5}$=$\frac{6}{5}$t��
�ٵ�0��t��$\frac{40}{13}$ʱ��
DQ=OA-OQ-AD=8-t-$\frac{8}{5}$t=8-$\frac{13}{5}$t��
��S=$\frac{1}{2}$DQ•CD=$\frac{1}{2}$��8-$\frac{13}{5}$t��•$\frac{6}{5}$t=-$\frac{39}{25}$t2+$\frac{24}{5}$t��
��-$\frac{b}{2a}$=$\frac{20}{13}$��0��$\frac{20}{13}$��$\frac{40}{13}$��
�൱t=$\frac{20}{13}$ʱ��S�����ֵΪ $\frac{48}{13}$��
�ڵ� $\frac{40}{13}$��t��5ʱ��
DQ=OQ+AD-OA=t+$\frac{8}{5}$t-8=$\frac{13}{5}$t-8��
��S=$\frac{1}{2}$DQ•CD=$\frac{1}{2}$�� $\frac{13}{5}$t-8��•$\frac{6}{5}$t=$\frac{39}{25}$t2-$\frac{24}{5}$t��
��-$\frac{b}{2a}$=$\frac{20}{13}$��$\frac{20}{13}$��$\frac{40}{13}$������S��t�����������
�൱t=5ʱ��S�����ֵΪ15��$\frac{48}{13}$��
����������S�����ֵΪ15��
���� ���⿼����Բ���ۺ��⣬��Ҫ�����˽�ֱ�������Σ����ɶ����������ε���������������ε��ж������ʣ����κ�������ֵ�����֪ʶ���ۺ��Խ�ǿ�����ѶȲ��ؼ�����Ҫ���ǵ�Q��D�����غ�ǰ�������������Ҳ�DZ������׳����ĵط���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�Ȳ�������Ҳ���Ǹ��� | B�� | ����ֵ��С������0 | ||
| C�� | һ�������������������Ƿ��� | D�� | ��a�ĵ�����$\frac{1}{a}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
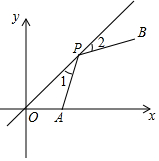 ��ͼ����ƽ��ֱ������ϵ�У���A��2��0������B��6��4������P��ֱ��y=x��һ�㣬����1=��2�����P�������ǣ�3��3����
��ͼ����ƽ��ֱ������ϵ�У���A��2��0������B��6��4������P��ֱ��y=x��һ�㣬����1=��2�����P�������ǣ�3��3�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com