

分析 (1)根据等腰直角三角形的性质可得出CD=BD,AD=CD,由此可得出结论;
(2)①根据题意画出图形即可;
②连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DE=DF.所以△DFE是等腰直角三角形;
③由割补法可知,四边形ECFD的面积保持不变.
解答 解:(1)CD=$\frac{1}{2}$AB.
∵在△ABC中,∠ACB=90°,BC=AC=10,
∴∠A=∠C=45°.
∵D是AB中点,
∴AD=BD,CD⊥AB,
∴∠BCD=∠B=45°,∠A=∠°,
∴CD=BD,AD=CD,即CD=$\frac{1}{2}$AB;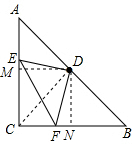
(2)①如图所示;
②连接CD,
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE和△CDF中,
$\left\{\begin{array}{l}CD=AD\\∠DCB=∠A\\ AE=CF\end{array}\right.$,
∴△ADE≌△CDF(SAS);
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形;
③不变.
分别过点D,作DM⊥AC,DN⊥BC,于点M,N,
∵∠ACB=90°,BC=AC=10,
∴AC=BC=5$\sqrt{2}$.
∵D是AB中点,
∴CM=AM=CN=BN=$\frac{5\sqrt{2}}{2}$,
∴S正方形CMDN=$\frac{5\sqrt{2}}{2}$•$\frac{5\sqrt{2}}{2}$=$\frac{25}{2}$.
在Rt△DEM与Rt△DFN中,
∵$\left\{\begin{array}{l}DE=DF\\ DM=DN\end{array}\right.$,
∴Rt△DEM≌Rt△DFN(HL),
∴四边形ECFD的面积等于正方形CMDN面积,即S四边形ECFD=$\frac{25}{2}$.
点评 此题主要考查了全等三角形的判定与性质以及正方形、等腰三角形、直角三角形性质以及勾股定理等知识.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2017届江苏省徐州市九年级下学期第一次(3月)月考数学试卷(解析版) 题型:单选题
二次函数y=x2﹣2x﹣1的顶点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
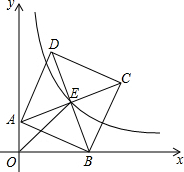 如图,直角坐标系中,点A、B是正半轴上两个动点,以AB为边作一正方形ABCD,对角线AC、BD的交点为E,若OE=2,则经过E点的双曲线为y=$\frac{2}{x}$.
如图,直角坐标系中,点A、B是正半轴上两个动点,以AB为边作一正方形ABCD,对角线AC、BD的交点为E,若OE=2,则经过E点的双曲线为y=$\frac{2}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.5×1010 | B. | 4.5×109 | C. | 4.5×108 | D. | 0.45×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | [a]+[-a]=0 | B. | [a]+[-a]等于0或-1 | C. | [a]+[-a]≠0 | D. | [a]+[-a]等于0或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm,3cm,5cm | B. | 3cm,3cm,6cm | C. | 5cm,8cm,2cm | D. | 4cm,5cm,6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com