
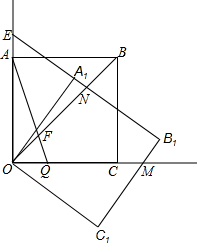
 如图,正方形ABCO中,点Q为OC边上的三等分点,连接AQ交对角线OB于点F.将正方形ABCO绕点按O顺时针方向旋转角α(0°<α<45°),得到正方形A1B1C1O.其中A1B1交对角线OB于点N,边B1C1交OC的延长线于点M,延长B1A1交OA的延长线于点E.若OF=2,AE=MB1,则四边形NOMB1的面积为$\frac{124}{7}$.
如图,正方形ABCO中,点Q为OC边上的三等分点,连接AQ交对角线OB于点F.将正方形ABCO绕点按O顺时针方向旋转角α(0°<α<45°),得到正方形A1B1C1O.其中A1B1交对角线OB于点N,边B1C1交OC的延长线于点M,延长B1A1交OA的延长线于点E.若OF=2,AE=MB1,则四边形NOMB1的面积为$\frac{124}{7}$. 分析 根据点Q为OC边上的三等分点,OF=2,可得正方形ABCO的边长为4$\sqrt{2}$;根据△C1OM≌△A1OE,可得CM=MB1,在Rt△OC1M中,根据(4$\sqrt{2}$)2+(4$\sqrt{2}$-x)2=(4$\sqrt{2}$+x)2,可得CM=MB1=$\sqrt{2}$=AE,再根据相似三角形的性质,可得CG=2$\sqrt{2}$,BG=2$\sqrt{2}$,ON=$\frac{40}{7}$,Rt△A1ON中,根据勾股定理可得A1N的长,最后根据S四边形NOMB1=S梯形A1B1MO-S△A1ON进行计算即可得到四边形NOMB1的面积.
解答 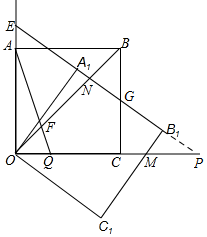 解:如图,延长EG交OC于P,
解:如图,延长EG交OC于P,
由OQ∥AB,可得△OQF∽△BAF,
∵点Q为OC边上的三等分点,OF=2,
∴$\frac{OF}{BF}$=$\frac{OQ}{BA}$,即$\frac{2}{BF}$=$\frac{1}{3}$,
∴BF=6,OB=8,
∴正方形ABCO的边长为4$\sqrt{2}$;
由旋转可得,∠C1=∠OA1E=90°,OC1=OA1,∠C1OM=∠A1OE,
∴△C1OM≌△A1OE,
∴OM=OE,
又∵OC=OA,
∴CM=AE,
又∵AE=MB1,
∴CM=MB1,
设CM=MB1=x,则C1M=4$\sqrt{2}$-x,OM=4$\sqrt{2}$+x,
在Rt△OC1M中,(4$\sqrt{2}$)2+(4$\sqrt{2}$-x)2=(4$\sqrt{2}$+x)2,
解得x=$\sqrt{2}$,
即CM=MB1=$\sqrt{2}$=AE,
由B1M∥OA1,可得$\frac{{B}_{1}M}{{A}_{1}O}$=$\frac{PB}{P{A}_{1}}$,即$\frac{\sqrt{2}}{4\sqrt{2}}$=$\frac{P{B}_{1}}{4\sqrt{2}+P{B}_{1}}$,
解得PB1=$\frac{4}{3}\sqrt{2}$,
∴Rt△B1PM中,PM=$\frac{5}{3}\sqrt{2}$,
由△PCG∽△PB1M,可得$\frac{CG}{{B}_{1}M}$=$\frac{CP}{{B}_{1}P}$,即$\frac{CG}{\sqrt{2}}$=$\frac{\frac{8}{3}\sqrt{2}}{\frac{4}{3}\sqrt{2}}$,
∴CG=2$\sqrt{2}$,BG=2$\sqrt{2}$;
由BG∥OE,可得△BGN∽△OEN,
∴$\frac{BG}{OE}$=$\frac{BN}{ON}$,即$\frac{2\sqrt{2}}{5\sqrt{2}}$=$\frac{8-ON}{ON}$,
解得ON=$\frac{40}{7}$,
∴Rt△A1ON中,A1N=$\sqrt{O{N}^{2}-{A}_{1}{O}^{2}}$=$\sqrt{(\frac{40}{7})^{2}-(4\sqrt{2})^{2}}$=$\frac{4}{7}\sqrt{2}$,
∴S四边形NOMB1=S梯形A1B1MO-S△A1ON
=$\frac{(\sqrt{2}+4\sqrt{2})×4\sqrt{2}}{2}$-$\frac{1}{2}$×4$\sqrt{2}$×$\frac{4}{7}\sqrt{2}$,
=20-$\frac{16}{7}$
=$\frac{124}{7}$.
故答案为:$\frac{124}{7}$.
点评 本题主要考查了旋转的性质,正方形的性质,全等三角形的判定与性质,勾股定理的运用以及相似三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造相似三角形,解题时灵活利用直角三角形勾股定理列方程求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 袋号 | ① | ② | ③ | ④ | ⑤ |
| 质量 | -5 | +3 | +9 | -1 | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com