y=

x-4或y=

x-4
分析:如图,D的坐标为(0,-4),过D的直线EF把正方形分成两部分,已知把正方形分成面积为2:1的两部分,那么四边形OEFA的面积是正方形面积的

或

.由于正方形的边长为6,所以正方形的面积为36,所以四边形OEFA的面积为12或24.设E的坐标为(a,0),那么OE=a,而OE∥AF,由此可以证明△OED∽△OFA,然后利用相似三角形的性质可以求出AF用a表示,然后利用梯形的面积公式可以列出关于a的方程,解方程即可求出a,也就求出了E的坐标,最后利用待定系数法求出直线的解析式.
解答:

解:如图,过D的直线EF把正方形分成两部分,
∵把正方形分成面积为2:1的两部分,
∴四边形OEFA的面积是正方形面积的

或

,
而正方形的边长为6,
∴正方形的面积为36,
∴四边形OEFA的面积为12或24.
设E的坐标为(a,0),
那么OE=a,
而OE∥AF,
∴△OED∽△OFA,
∴OE:AF=OD:OA,
而正方形的边长为6,D的坐标为(0,-4),
∴AF=

a,
∴S
四边形OEFA=

=12或S
四边形OEFA=

=24,
∴a=

或

,
∴E(

,0)或(

,0),而D的坐标为(0,-4),
设所求直线DE的解析式为y=kx+b,
∴
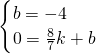
或
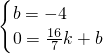
,
∴y=

x-4或y=

x-4.
点评:此题主要考查了待定系数法求直线的解析式,当不是直接利用已知点的坐标,而是利用正方形的性质和相似三角形的性质求出线段,再求出相关的点坐标,最后求出直线的解析式.

 如图,正方形的边长为6,经过点(0,-4)的直线,把正方形分成面积为2:1的两部分,则直线的函数解析式________.
如图,正方形的边长为6,经过点(0,-4)的直线,把正方形分成面积为2:1的两部分,则直线的函数解析式________. x-4或y=
x-4或y= x-4
x-4 或
或 .由于正方形的边长为6,所以正方形的面积为36,所以四边形OEFA的面积为12或24.设E的坐标为(a,0),那么OE=a,而OE∥AF,由此可以证明△OED∽△OFA,然后利用相似三角形的性质可以求出AF用a表示,然后利用梯形的面积公式可以列出关于a的方程,解方程即可求出a,也就求出了E的坐标,最后利用待定系数法求出直线的解析式.
.由于正方形的边长为6,所以正方形的面积为36,所以四边形OEFA的面积为12或24.设E的坐标为(a,0),那么OE=a,而OE∥AF,由此可以证明△OED∽△OFA,然后利用相似三角形的性质可以求出AF用a表示,然后利用梯形的面积公式可以列出关于a的方程,解方程即可求出a,也就求出了E的坐标,最后利用待定系数法求出直线的解析式. 解:如图,过D的直线EF把正方形分成两部分,
解:如图,过D的直线EF把正方形分成两部分, 或
或 ,
, a,
a, =12或S四边形OEFA=
=12或S四边形OEFA= =24,
=24, 或
或 ,
, ,0)或(
,0)或( ,0),而D的坐标为(0,-4),
,0),而D的坐标为(0,-4),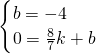 或
或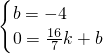 ,
, x-4或y=
x-4或y= x-4.
x-4.

 初中暑期衔接系列答案
初中暑期衔接系列答案 +b+c的正方形来研究.
+b+c的正方形来研究.