
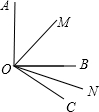
 如图所示.
如图所示. 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
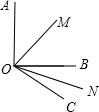 如图所示.
如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
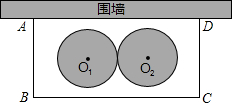 某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:
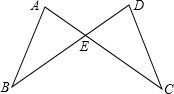 为参加学校举行的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AC=DB,AC,BD交于点E.你认为小明扎的风筝两脚的大小相同吗?(即∠B=∠C吗),试说明理由.
为参加学校举行的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AC=DB,AC,BD交于点E.你认为小明扎的风筝两脚的大小相同吗?(即∠B=∠C吗),试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给出的数据求树高ED.
为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给出的数据求树高ED.查看答案和解析>>
科目:初中数学 来源: 题型:
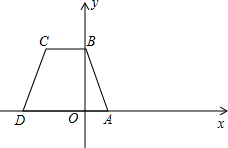 若不存在,请说明理由.
若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com