
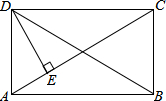
 如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{2}$∠CDE,那么∠BDC的度数为30°.
如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{2}$∠CDE,那么∠BDC的度数为30°. 分析 由矩形的性质得出∠ADC=90°,OA=OD,得出∠ODA=∠DAE,由已知条件求出∠ADE,得出∠DAE、∠ODA,即可得出∠BDC的度数.
解答 解:如图所示: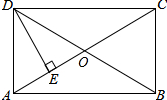 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠ADC=90°,OA=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OD,
∴∠ODA=∠DAE,
∵∠ADE=$\frac{1}{2}$∠CDE,
∴∠ADE=$\frac{1}{3}$×90°=30°,
∵DE⊥AC,
∴∠AED=90°,
∴∠DAE=60°,
∴∠ODA=60°,
∴∠BDC=90°-60°=30°;
故答案为:30°.
点评 本题考查了矩形的性质、等腰三角形的判定与性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
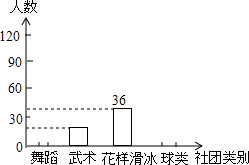 某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | b | 25% |
| 武术 | 24 | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | a | 50% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×10-6 | B. | 25×10-5 | C. | 2.5×10-4 | D. | 2.5×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
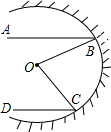 如图是汽车灯的剖面图,从O点发出的光纤照射到凹面镜上,反射出的光线BA、CD是互相平行的水平线,若∠DCO=50°,∠ABD=α,则∠BOC的度数为50°+α(用含α的式子表示).
如图是汽车灯的剖面图,从O点发出的光纤照射到凹面镜上,反射出的光线BA、CD是互相平行的水平线,若∠DCO=50°,∠ABD=α,则∠BOC的度数为50°+α(用含α的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
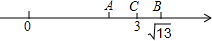 如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )
如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )| A. | 6-$\sqrt{13}$ | B. | 3-$\sqrt{13}$ | C. | $\sqrt{13}$-3 | D. | -$\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com