
分析 (1)分子是从1开始连续的自然数,分母比分子多1,奇数位置为负,偶数位置为正,再由-$\frac{1}{2}$+$\frac{2}{3}$=$\frac{1}{6}$=$\frac{1}{2×3}$,-$\frac{3}{4}$+$\frac{4}{5}$=$\frac{1}{20}$=$\frac{1}{4×5}$得出相邻两个数的和的分母是这两个数的分母的乘积,分子是1,符号取决于绝对值的大的符号,由此规律解决问题;
(2)利用(1)中的规律得出第2015个数与2016个数,进一步求和得出答案即可.
解答 解:(1)-$\frac{1}{2}$+$\frac{2}{3}$=$\frac{1}{6}$=$\frac{1}{2×3}$,-$\frac{3}{4}$+$\frac{4}{5}$=$\frac{1}{20}$=$\frac{1}{4×5}$;
(2)第2015个数是-$\frac{2015}{2016}$,第2016个数是$\frac{2016}{2017}$,
-$\frac{2015}{2016}$+$\frac{2016}{2017}$=$\frac{1}{2016×2017}$=$\frac{1}{4066272}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律,解决问题.


科目:初中数学 来源: 题型:选择题
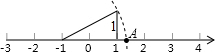 如图所示:数轴上点A所表示的数为a,则a的值是( )
如图所示:数轴上点A所表示的数为a,则a的值是( )| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | -$\sqrt{5}$+1 | D. | -$\sqrt{5}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD中,AC、BD交于点O1,作?BCD1O1,连结BD1交AC于点O2,作?BCD2O2,连结BD2交AC于点O3,…以此类推,若AC⊥AD,AD=1,∠ADC=60°,则?BCDnOn的面积是$\frac{\sqrt{3}}{{2}^{n}}$.
如图,?ABCD中,AC、BD交于点O1,作?BCD1O1,连结BD1交AC于点O2,作?BCD2O2,连结BD2交AC于点O3,…以此类推,若AC⊥AD,AD=1,∠ADC=60°,则?BCDnOn的面积是$\frac{\sqrt{3}}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),
已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com