
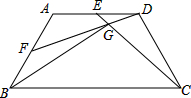
 如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$.
如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$. 分析 延长DF、CB交于点H,过G作LM⊥BC于M,DN⊥BC于N,易证△HBF≌△DAF≌△CDE,得到BH=AD,HF=DF,由△DEG∽△CHG,得出$\frac{DG}{HG}=\frac{DE}{CH}=\frac{1}{6}$,设DE=x,则DC=2x,NC=x,DN=$\sqrt{3}$x,由△HMG∽△HND,得出MG=$\frac{6\sqrt{3}x}{7}$,HN=5x,HM=$\frac{30}{7}$x,BM=$\frac{16}{7}$x,在Rt△HMG中,根据勾股定理求得:x2=7,在Rt△BGM中,BG2=BM2+GM2=$\frac{52}{7}$x2=52,即可得到BG的长.
解答 解:延长DF、CB交于点H,过G作LM⊥BC于M,DN⊥BC于N,
∵AD∥BC,∠A=120°,AB=AD=CD,
∴BC=2AD,
∵点E、点F分别为线段AD、AB的中点,
∴AF=BF=DE,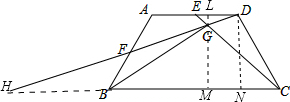
易证△HBF≌△DAF≌△CDE,
∴BH=AD,HF=DF,
∵AD∥BC,
∴△DEG∽△CHG,
∴$\frac{DG}{HG}=\frac{DE}{CH}=\frac{1}{6}$,
设DE=x,则DC=2x,NC=x,DN=$\sqrt{3}$x,
∵△HMG∽△HND,
∴MG=$\frac{6\sqrt{3}x}{7}$,HN=5x,HM=$\frac{30}{7}$x,BM=$\frac{16}{7}$x,
在Rt△HMG中,根据勾股定理求得:x2=7,
在Rt△BGM中,
BG2=BM2+GM2=$\frac{52}{7}$x2=52.
∴BG=2$\sqrt{13}$.
点评 本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理的综合运用,通过辅助线构造全等和相似是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 西宁 | 门源 | 36元 | 30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
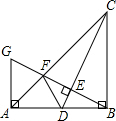 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①$\frac{AG}{AB}=\frac{FG}{FB}$;②FG=$\frac{1}{2}$FB;③AF=$\frac{\sqrt{2}}{3}AB$;④S△ABC=5S△BDF,其中正确结论的序号是①②③.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①$\frac{AG}{AB}=\frac{FG}{FB}$;②FG=$\frac{1}{2}$FB;③AF=$\frac{\sqrt{2}}{3}AB$;④S△ABC=5S△BDF,其中正确结论的序号是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
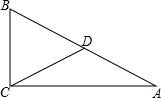 如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于$\frac{8\sqrt{5}}{5}$.
如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于$\frac{8\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com