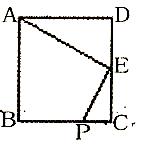
解:(1)证明:如图①,∵ BD⊥AC,∠ABC=90°,∠ADB=∠ABC,
又∵∠A=∠A,∴△ADB∽△ABC 。
∴

,∴ AB
2=AD·AC。
(2)如图②,过点C作CG⊥AD交AD的延长线于点G。

∵ BE⊥AD,∴∠CGD=∠BED=90°,CG∥BF。
又∵

,
∴AB=BC=2BD=2DC,BD=DC。
又∵∠BDE=∠CDG,∴△BDE≌△CDG(AAS)。
∴ED=GD=
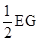
。
由(1)可得:AB
2=AE·AD,BD
2=DE·AD,
∴
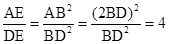
。∴ AE=4DE。∴

。
又∵CG∥BF,∴

。
(3) ①当点D在BC边上时,

的值为n
2+n;
②当点D在BC延长线上时,

的值为n
2-n;
③当点D在CB延长线上时,

的值为n-n
2。
(1)由证△ADB∽△ABC即可得到结论。
(2)过点C作CG⊥AD交AD的延长线于点G,由已知用AAS证△BDE≌△CDG,得到EF是△ACG的中位线,应用(1)的结论即可。
(3)分点D在BC边上、点D在BC延长线上和点D在CB延长线上三种情况讨论:
①当点D在BC边上时,如图3,过点C作CG⊥AD交AD的延长线于点G。
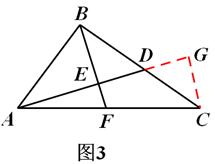
∵ BE⊥AD,∴∠CGD=∠BED=90°,CG∥BF。
∴△BDE∽△CDG。∴

。
又∵

,∴
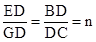
∴AB=nBC,BD=nDC,ED=nGD。
∴BC=(n+1)DC,EG=
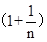
ED。
由(1)可得:AB
2=AE·AD,BD
2=DE·AD,
∴
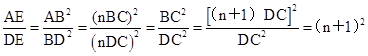
。∴ AE=
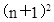
DE。
∴
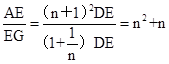
。
又∵CG∥BF,∴
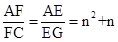
。
②当点D在BC延长线上时,如图4,过点C作CH⊥AD交AD于点H。
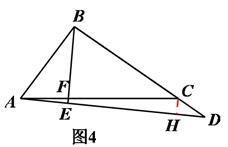
∵ BE⊥AD,∴∠CHD=∠BED=90°,CH∥BF。
∴△BDE∽△CDH。∴
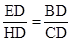
又∵

,∴

∴AB=nBC,BD=nDC,ED=nHD。
∴BC=(n-1)DC,EH=
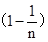
ED。
由(1)可得:AB
2=AE·AD,BD
2=DE·AD,
∴
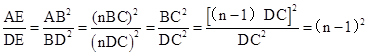
。∴ AE=

DE。
∴

。
又∵CH∥BF,∴
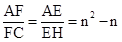
。
③当点D在CB延长线上时,如图5,过点C作CI⊥AD交DA的延长线于点I。
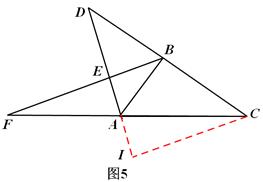
∵ BE⊥AD,∴∠CID=∠BED=90°,CI∥BF。
∴△BDE∽△CDI。∴

又∵

,∴
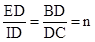
∴AB=nBC,BD=nDC,ED=nID。
∴BC=(1-n)DC,EI=
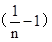
ED。
由(1)可得:AB
2=AE·AD,BD
2=DE·AD,
∴

。∴ AE=

DE。
∴
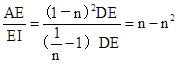
。
又∵CI∥BF,∴

。

 ,求
,求 的值;
的值; ,请探究并直接写出
,请探究并直接写出 的所有可能的值(用含n的式子表
的所有可能的值(用含n的式子表
 的值为n2+n;②当点D在BC延长线上时,
的值为n2+n;②当点D在BC延长线上时, 的值为n2-n;③当点D在CB延长线上时,
的值为n2-n;③当点D在CB延长线上时, 的值为n-n2。
的值为n-n2。 ,∴ AB2=AD·AC。
,∴ AB2=AD·AC。
 ,
,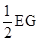 。
。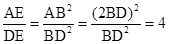 。∴ AE=4DE。∴
。∴ AE=4DE。∴ 。
。 。
。 的值为n2+n;
的值为n2+n; 的值为n2-n;
的值为n2-n; 的值为n-n2。
的值为n-n2。
 。
。 ,∴
,∴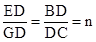
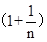 ED。
ED。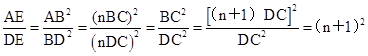 。∴ AE=
。∴ AE=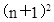 DE。
DE。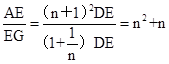 。
。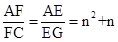 。
。
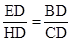
 ,∴
,∴
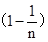 ED。
ED。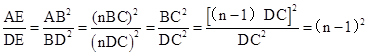 。∴ AE=
。∴ AE= DE。
DE。 。
。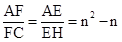 。
。

 ,∴
,∴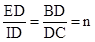
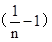 ED。
ED。 。∴ AE=
。∴ AE= DE。
DE。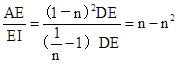 。
。 。
。