Question

12．如图1，抛物线y=$\frac{1}{2}$x²+c与x轴交于A，B两点（A在B的左侧），与y轴交于C，且AB=2OC，
（1）求c的值；
（2）P（m，n）是抛物线上一动点，过P点作直线L交y轴于Q（0，s），且直线L和抛物线只有唯一公共点，求n+s的值；
（3）如图2，E为直线y=3上的一动点，CE交抛物线于D，EF∥y轴交抛物线于F，求证：直线FD经过y轴上一定点，并求定点坐标．

Answer 1

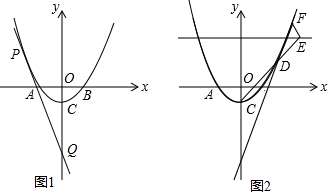
分析 （1）由题意可知：OC=-c，AB=-2c，令y=0代入抛物线的解析式也可求出AB=2$\sqrt{-2c}$，列出方程即可求出c的值；
（2）根据P与Q的坐标求出PQ的直线解析式，然后与抛物线联立方程求出△，令△=0后进行化简，即可求出n与s的值；
（3）设E（a，3），F（a，b），然后求出直线CE的解析式，与抛物线联立方程求出D的坐标，最后求出直线DF的解析式即可求出该定点．

解答 解：（1）由题意可知：c＜0，
∴OC=-c，
∴AB=-2c，
令y=0代入y=$\frac{1}{2}$x²+c，
∴x²=-2c，
∴x=±$\sqrt{-2c}$，
∴AB=2$\sqrt{-2c}$，
∴-2c=c²，
∴c=0（舍去）或c=-2，
∴抛物线的解析式为：y=$\frac{1}{2}$x²-2；
（2）设直线PQ的解析式为：y=k₁x+b₁，
将P（m，n）与Q（0，s）代入y=k₁x+b₁，
可得：$\left\{\begin{array}{l}{n=m{k}_{1}+{b}_{1}}\\{{b}_{1}=s}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{k}_{1}=\frac{n-s}{m}}\\{{b}_{1}=s}\end{array}\right.$，
∴直线PQ的解析式为：y=$\frac{n-s}{m}$x+s
联立$\left\{\begin{array}{l}{y=\frac{n-s}{m}x+s}\\{y=\frac{1}{2}{x}^{2}-2}\end{array}\right.$，

化简可得：$\frac{1}{2}$x²-$\frac{n-s}{m}$x-2-s=0，
∴△=（$\frac{n-s}{m}$）²-4×$\frac{1}{2}$（-2-s）=0，
∴化简可得：n²+4n+s²+4s+8=0，
∴（n+2）²+（s+2）²=0，
∴n=-2，s=-2，
∴n+s=-4；
（3）设E（a，3），F（a，$\frac{1}{2}{a}^{2}$-2），
设直线CE的解析式为：y=k₂x+b₂，
把C（0，-2）和E（a，3）代入y=k₂x+b₂，
可得：$\left\{\begin{array}{l}{{b}_{2}=-2}\\{3=a{k}_{2}+{b}_{2}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{k}_{2}=\frac{5}{a}}\\{{b}_{2}=-2}\end{array}\right.$，
∴直线CE的解析式为：y=$\frac{5}{a}$x-2，
∴联立$\left\{\begin{array}{l}{y=\frac{5}{a}x-2}\\{y=\frac{1}{2}{x}^{2}-2}\end{array}\right.$，
解得：x=0（舍去）或x=$\frac{10}{a}$，
∴D（$\frac{10}{a}$，$\frac{50-2{a}^{2}}{{a}^{2}}$），
设直线DF的解析式为：y=k₃x+b₃，
把D和F的坐标分别代入y=k₃x+b₃
可得：${\left\{\begin{array}{l}{\frac{50-2{a}^{2}}{{a}^{2}}=\frac{10}{a}{k}_{3}+{b}_{3}}\\{\frac{1}{2}{a}^{2}-2=a{k}_{3}+{b}_{3}}\end{array}\right.}_{\;}$，
解得：$\left\{\begin{array}{l}{{k}_{3}=\frac{10+{a}^{2}}{2a}}\\{{b}_{3}=-7}\end{array}\right.$，
∴直线DF的解析式为：y=$\frac{10+{a}^{2}}{2a}$x-7，
令x=0代入y=$\frac{10+{a}^{2}}{2a}$x-7，
∴y=-7，
∴直线DF恒过点（0，-7）

点评 本题考查二次函数综合问题，涉及待定系数法求解析式，一元二次方程和方程组的解法，分式的混合运算，综合程度加高，计算量较大．