练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列调查中，调查方式不合理的是（　　）
    A．用抽样调查了解广州市中学生每周使用手机所用的时间
    B．用全面调查了解某班学生对6月5日是“世界环境日”的知晓情况
    C．用抽样调查选出某校短跑最快的学生参加全市比赛
    D．用抽样调查了解南沙区初中学生零花钱的情况

    分析 根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似解答．

    解答 解：用抽样调查了解广州市中学生每周使用手机所用的时间调查方式合理，A错误；
    用全面调查了解某班学生对6月5日是“世界环境日”的知晓情况调查方式合理，B错误；
    用抽样调查选出某校短跑最快的学生参加全市比赛调查方式不合理，C正确；
    用抽样调查了解南沙区初中学生零花钱的情况调查方式合理，D错误，
    故选：C．

    点评 本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知方程mx+ny=5的两个解是$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$和$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$
    （1）求m、n的值；
    （2）用含有x的代数式表示y；
    （3）若y是不小于-2的负数，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：（π-2016）0+（$\frac{1}{3}$）-1-$\sqrt{4}$×|-3|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，直线y=$\frac{1}{2}$x+2分别与x轴、y轴相交于点A、点B．
    （1）求点A和点B的坐标；
    （2）若点P是y轴上的一点，设△AOB、△ABP的面积分别为S△AOB与S△ABP，且S△ABP=2S△AOB，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

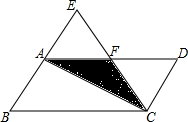    15．如图，在平行四边形ABCD中，BC=6cm，将△ABC沿对角线AC折叠，点B的对应点落在点E处，BC边的对应边CE与AD边交于点F，此时△CDF为等边三角形．
    （1）求AB的长．
    （2）求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

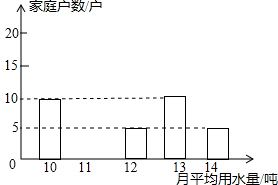    5．为了倡导“节约用水，从我做起”，南沙区政府决定对区直属机关300户家庭的用水情况作一次调查，区政府调查小组随机抽查了其中50户家庭一年的月平均用水量（单位：吨），调查中发现每户用水量均在10-14吨/月范围，并将调查结果制成了如图所示的条形统计图．
    （1）请将条形统计图补充完整；
    （2）这50户家庭月用水量的平均数是11.6，众数是11，中位数是11；
    （3）根据样本数据，估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．数学老师布置了这样一道作业题：
    在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，α+β=120°，连接AD，求∠ADB的度数．
    小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α=90°，β=30°时（如图1），利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形的相关知识便可解决这个问题．

    （1）请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；
    （2）结合小聪研究特殊问题的启发，请解决数学老师布置的这道作业题；
    （3）解决完老师布置的这道作业题后，小聪进一步思考，当点D和点A在直线BC的异侧时，且∠ADB的度数与（1）中相同，则α，β满足的条件为0°＜α＜180°，β=60°或120°＜α＜180°，α-β=120°（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于F，射线CE交射线OB于G．
    （1）如图①，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系：CF=CG；
    （2）如图②，若∠AOB=120°，∠DCE=∠AOC，试判断线段CF与线段CG的数量关系并加以证明；
    （3）若∠AOB=α，当∠DCE满足什么条件时，你在（2）中得到的结论仍然成立，请直接写出∠DCE满足的条件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

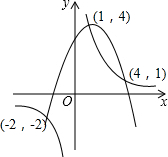    4．二次函数y=ax2+bx+c（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象相交（如图），则不等式ax2+bx+c＞$\frac{k}{x}$的解集是（　　）
    A．1＜x＜4或x＜-2B．1＜x＜4或-2＜x＜0
    C．0＜x＜1或x＞4或-2＜x＜0D．-2＜x＜1或x＞-4

    查看答案和解析>>

    同步练习册答案