
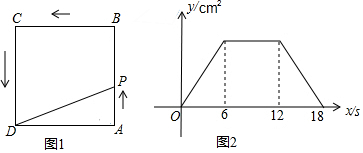
分析 (1)从图2中看到刚好6s时y最大,得到点P在AB上运动的时间,从而得到AB,x=17时,点P在CD边上,且PD=1即可;
(2)由图2面积没变的是中间一段,从而得到点P在BC上时,y值不变;
拓展:先判断点P在那段线段上运动,用三角形的面积公式计算即可;
探究:y是15时,得到点P在AB和CD这两段线段上,所以直接代入函数关系式中即可.
解答 解:(1)由图2,得到点P在AB上运动时间为6,
∵点P以1cm/s的速度运动,
∴AB=6÷1=6,
∵正方形ABCD,
∴AB=BC=CD=6,
当x=17(s)时,点P在线段CD上,PD=1,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×1=3,
故答案为6,3,
(2)当点P在线段 BC上运动时,y的值保持不变.理由如下:
∵△PAD的边AD时定值6,
∴点P到AD的距离不变时,△PAD的面积不变,
∴点P在BC上,
故答案为:BC;
拓展:当0<x<6时,点P在线段AB上,PD=x,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×x=3x,
当12<x<18时,点P在线段CD上,PD=18-x,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×(18-x)=54-3x,
探究:∵y的值等于15cm2?
把y=15代入y=3x中,得15=3x,
∴x=5,
把y=15代入y=54-3x中,得15=54-3x,
∴x=13,
∴当x=5s或13s时,y的值等于15.
点评 此题是四边形综合题,主要考查的是动点问题、正方形的性质、三角形面积的计算、函数关系式以及图象等知识,解本题的关键是从图中找到对应的量,也是解本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.
星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
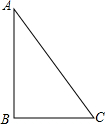 如图,Rt△ABC中,∠B=90°,AB=3,AC=5.
如图,Rt△ABC中,∠B=90°,AB=3,AC=5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)
如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
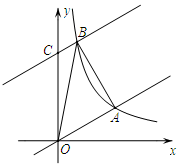 如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).
如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
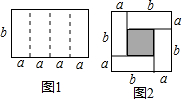 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com