
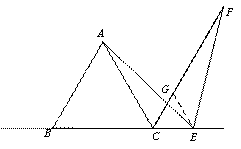
【探究发现】如图1, 是等边三角形,
是等边三角形, ,EF交等边三角形外角平分线CF所在的直线于点F.当点E是BC的中点时,有AE=EF成立;
,EF交等边三角形外角平分线CF所在的直线于点F.当点E是BC的中点时,有AE=EF成立;
【数学思考】某数学兴趣小组在探究AE、EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点E是直线BC上(B,C除外)任意一点时(其它条件不变),结论AE=EF仍然成立.
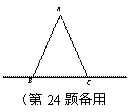
假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任 意一点”;“点E是线段BC延长线上的任意一点”;“ 点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并进行证明.
意一点”;“点E是线段BC延长线上的任意一点”;“ 点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并进行证明.
 | |||
 | |||

【拓展应用】当点E在线段BC的延长线上时,若CE = BC,在备用图2中画出图形,并运用上述结论求出 的值.
的值.
(1) 正确画出图形
①第一种情况:当点E在线段 BC上时.
BC上时.
证明:在AB上取AG=CE,连接EG.
则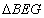 是等边三角形
是等边三角形
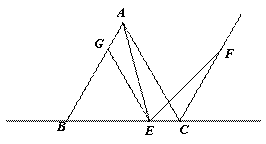
∴∠AGE=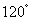 ,而∠ECF=
,而∠ECF=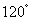
∴∠AGE=∠ECF…
∵∠AEC=∠AEF+∠CEF=∠GAE+∠B,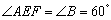
 ∴∠GAE=∠CEF
∴∠GAE=∠CEF
∴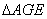 ≌
≌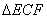 (ASA)
(ASA)
∴AE=EF
②第二种情况:当点E在BC延长线上时.
在CF取CG=CE,连接EG.
∵CF是等边三角形外角平分线
∴∠ECF=
 ∵CG=CE
∵CG=CE
∴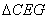 是等边三角形
是等边三角形
∴∠FGE=∠ACE=
∵∠AEF=∠AEG+∠GEF=∠AEG+∠AEC=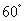
∴∠GEF=∠CEA…
∴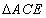 ≌
≌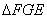 (ASA)
(ASA)
∴AE=EF
③第三种情况:当点E在BC的反向延长线上时.
在AB的延长线上取AG=CE,连接EG.
则有BG= BE;∴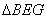 是等边三角形
是等边三角形
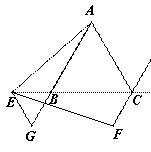 ∴∠G=∠ECF=
∴∠G=∠ECF=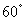
∵∠CEF=∠AEF-∠AEC=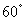 -∠AEC
-∠AEC
∠EAB=∠ABC-∠AEC=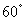 -∠AEC
-∠AEC
∴∠CEF=∠EAB
∴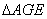 ≌
≌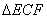 (ASA)
(ASA)
∴AE=EF
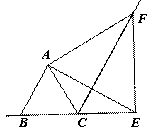 (2)正确画出图形…
(2)正确画出图形…
∵CE = BC=AC
∴∠CAE=∠CEA=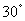 ,∠BAE=
,∠BAE=
∴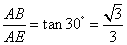
∵AE=EF,∠AEF=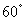
∴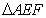 是等边三角形
是等边三角形
∴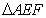 ∽
∽
∴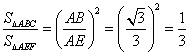 .
.


科目:初中数学 来源: 题型:
三个小球上分别标有-2,0,1三个数,这三个球除了标的数不同外,其余均相同.将
小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸
出一个小球,再记下小球上所标之数.求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于-4,平方和等于14,求:这13次摸球中,摸到球上所标之数是0的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
市运会举行射击比赛,某校射击队从甲、乙、丙、丁四人中选拔一人参赛.在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如右表.请你根据表中数据选一人参加比赛,最合适的人选是 .
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 8.2 | 8.0 | 8.2 | 8.0 |
| 方差 | 2.0 | 1.8 | 1.5 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
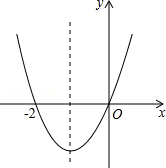
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:
①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com