
 小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:分析 (1)根据客厅面积为6m米2,卫生间面积为2n米2,厨房面积为2×(6-3)=6米2,卧室面积为3×(2+2)=12米2,把它们的面积相加即可得出地面总面积为;
(2)根据客厅面积是卫生间面积的8倍和卫生间、卧室、厨房面积的和比客厅还少3平方米,列出方程组,求出m,n的值,求出地面的总面积,再利用单价×面积即可求得总费用.
解答 解:(1)根据题意得:
地面的总面积S=6m+2n+2×(6-3)+3×(2+2)=6m+2n+18(米2);
(2)依题意可列方程组
$\left\{\begin{array}{l}{2n×8=6m}\\{12+2n+6=6m-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=\frac{3}{2}}\end{array}\right.$,
S=6m+2n+18=6×4+2×$\frac{3}{2}$+18=45(米2),.
总费用为45×100=4500(元).
点评 本题考查了二元一次方程组的应用,关键是根据长方形的面积公式求出各部分的面积,再利用单价×面积求出总费用.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,试说明一下论断正确的理由:
已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,试说明一下论断正确的理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
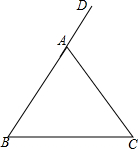 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角,AM是∠DAC的平分线,AC的垂直平分线与AM交于点F,与BC边交于点E,连接AE、CF.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角,AM是∠DAC的平分线,AC的垂直平分线与AM交于点F,与BC边交于点E,连接AE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的弦,D为⊙O上不与A、B重合的一点,DC⊥AB于点C,$\widehat{AM}$=$\widehat{BM}$,连结DM,求证:∠CDM=∠ODM.
如图,AB是⊙O的弦,D为⊙O上不与A、B重合的一点,DC⊥AB于点C,$\widehat{AM}$=$\widehat{BM}$,连结DM,求证:∠CDM=∠ODM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com