
 如图,二次函数y=ax2+bx+c的图象与x轴交于点A(6,0)和点B(2,0),与y轴交于点C(0,2$\sqrt{3}$),⊙P经过点A、B、C三点.
如图,二次函数y=ax2+bx+c的图象与x轴交于点A(6,0)和点B(2,0),与y轴交于点C(0,2$\sqrt{3}$),⊙P经过点A、B、C三点.分析 (1)由二次函数y=ax2+bx+c的图象与x轴交于点A(6,0)和点B(2,0),首先设二次函数的表达式为:y=a(x-6)(x-2),然后将点C(0,2$\sqrt{3}$)代入,即可求得二次函数的表达式;
(2)首先过点P作PD⊥x轴于点D,由垂径定理即可求得点P的横坐标,然后设点P的坐标为(4,y),由PB=PC,可得方程42+(y-2$\sqrt{3}$)2=22+y2,解此方程即可求得答案;
(3)首先过点P作PQ∥x轴,交二次函数在第一象限内的图象上点Q,即可求得点Q的坐标,证得PQ=AB,可得四边形ABPQ是平行四边形,又由PB=AB=4,证得四边形ABPQ是菱形.
解答 解:(1)设二次函数的表达式为:y=a(x-6)(x-2),
∵二次函数与y轴交于点C(0,2$\sqrt{3}$),
∴12a=2$\sqrt{3}$,
解得:a=$\frac{\sqrt{3}}{6}$,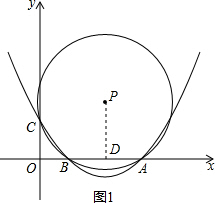 ∴y=$\frac{\sqrt{3}}{6}$(x-6)(x-2)=$\frac{\sqrt{3}}{6}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$;
∴y=$\frac{\sqrt{3}}{6}$(x-6)(x-2)=$\frac{\sqrt{3}}{6}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$;
(2)如图1,过点P作PD⊥x轴于点D,
∴AD=BD,
∵点A(6,0)和点B(2,0),
∴AB=6-2=4,
∴BD=AD=2,
∴OD=OB+BD=4,
设点P的坐标为(4,y),
∵⊙P经过点A、B、C三点,C(0,2$\sqrt{3}$),
∴PC=PB,
∴42+(y-2$\sqrt{3}$)2=22+y2,
解得:y=2$\sqrt{3}$,
∴点P的坐标为:(4,2$\sqrt{3}$); (3)存在.
(3)存在.
如图2,过点P作PQ∥x轴,交二次函数在第一象限内的图象上点Q,
则此时Q的纵坐标为2$\sqrt{3}$,
∴$\frac{\sqrt{3}}{6}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$=2$\sqrt{3}$,
解得:x=8,
∴点Q的坐标为:(8,2$\sqrt{3}$),
且PQ=AB=4,
∴四边形ABPQ是平行四边形,
∵PB=AB=4,
∴四边形ABPQ是菱形.
点评 此题属于二次函数的综合题,考查了待定系数法求二次函数的解析式、垂径定理、平行四边形的判定与性质以及菱形的判定等知识.注意准确作出辅助线,利用方程思想求解是解此题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解我省2015年6月份九年级学生中考数学的成绩情况 | |
| B. | 了解全国高血压患者使用“尼福达”的情况 | |
| C. | 了解我校七年级(4)班学生的视力情况 | |
| D. | 了解我市20-30岁青年的文化水平(学历)情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是边长为5的正方形,点G是BC上的一点,DE⊥AG于点E,BF∥DE,且交AG于点F.若E是AF的中点,则BF的长为$\sqrt{5}$.
如图,四边形ABCD是边长为5的正方形,点G是BC上的一点,DE⊥AG于点E,BF∥DE,且交AG于点F.若E是AF的中点,则BF的长为$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com