
分析 先设x+3y=m,x-3y=n,再因式分解后进行解答即可.
解答 解:设x+3y=m,x-3y=n,可得$\left\{\begin{array}{l}{{x}^{2}-9{y}^{2}=15}\\{x+3y=5}\end{array}\right.$变形为$\left\{\begin{array}{l}{mn=15}\\{m=5}\end{array}\right.$,
解得:m=5,n=3,
所以可得$\left\{\begin{array}{l}{x+3y=5}\\{x-3y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=\frac{1}{3}}\end{array}\right.$.
点评 此题考查高次方程的解法,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
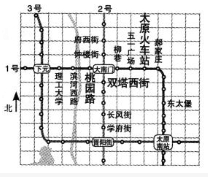 如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )
如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )| A. | (0,1) | B. | (-3,-1) | C. | (0,-1) | D. | (-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com