
 如图,直线y=
如图,直线y=| 3 |
| 4 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
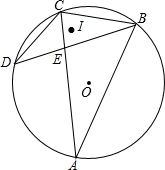 如图,已知△BAC,AB=AC,O为△ABC外心,D为⊙O上一点,BD与AC的交点为E,且BC2=AC•CE
如图,已知△BAC,AB=AC,O为△ABC外心,D为⊙O上一点,BD与AC的交点为E,且BC2=AC•CE| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某公司想了解一款品牌运动服的销售情况来决定下一步的生产数量.该公司随机统计了某天各个摊位销售这款不同颜色的运动服的销售数量,并绘制成统计表和扇形统计图(如图).
某公司想了解一款品牌运动服的销售情况来决定下一步的生产数量.该公司随机统计了某天各个摊位销售这款不同颜色的运动服的销售数量,并绘制成统计表和扇形统计图(如图).| 颜色 | 红 | 白 | 蓝 | 绿 | 黑 | 五彩 |
| 销售量(件) | 18 | 18 | 15 | 19 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,茗茗从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用(15,10)表示,那么(-10,5)表示的位置是( )
如图,茗茗从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用(15,10)表示,那么(-10,5)表示的位置是( )| A、点A | B、点B | C、点C | D、点D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com