
����Ŀ�������仯�����Ѿ�����������ĸ߶ȹ�ע���йز�����ȫ����Χ�ڶ�12��35��������Ⱥ�����˼�����������飬���Ƴ���������ͳ��ͼ��

�����ͼ�е���Ϣ���ش��������⣺
��1����γ��������й������������ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ��18��23�겿�ֵ�Բ�ĽǵĶ�����������
��4���ݱ�����Ŀǰ�ҹ�12��35���������ԼΪ2000�����������12��23�������
���𰸡�(1)a=300��(2)108����(3)12��23�������Ϊ400��
�������������������1������30-35�����������ռ�İٷֱ�������������
��2���ӵ�����������м�ȥ��֪����������������ɵõ�12-17����������ݴ˲�ȫ����ͳ��ͼ��
��3���ȼ���18-23�������ռ�����������İٷֱȣ��ټ�����һ������Ӧ��Բ�ĽǵĶ�����
��4���ȼ��������12��23���������ռ�İٷֱȣ������������ԼΪ2000���е�12��23���������
����������⣺��1���������ͳ��ͼ������ͳ��ͼ��֪��30-35�������Ϊ330�ˣ���ռ�İٷֱ�Ϊ22%�����Ե����������Ϊ330��22%=1500�ˣ�
�ʴ�Ϊ��1500 ��
��2��1500-450-420-330=300�ˣ�
��ȫ������ͳ��ͼ��ͼ��

��3��18-23����һ������Ӧ��Բ�ĽǵĶ���Ϊ360��![]() =108����
=108����
�ʴ�Ϊ��108�� ��
��4����300+450����1500=50%��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���ʽ��21=2��22=4��23=8��24=16��25=32��26=64��27=128��28=256��������������ʽ�Ĺ��ɣ���ô22018�ĸ�λ������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAC=90����BD��DE��CE��DE�����������������Բ���ʹ��ABD�ա�CAE�������ǣ�������
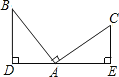
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ��ʹһ�������λ֧��ABCDEF�ȹ��Ҳ����Σ�������Ҫ����_____��ľ�����̶ܹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������Ϊ��ϣ��������ļ�����ݣ�ȫ��ƱΪÿ��18Ԫ��ѧ�����ܰ�ۣ�ij���ݳ����۳�966��Ʊ������15480Ԫ�����ⳡ�ݳ����۳�ѧ��Ʊ�����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�У�EΪ�Խ���BD��һ�㣬��E����EF��BD��BC��F������DF��GΪDF�е㣬����EG��CG��
��1����֤��EG=CG��
��2����ͼ���С�BEF��B����ʱ����ת45�㣬��ͼ����ʾ��ȡDF�е�G������EG��CG���ʣ�1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����ͼ���С�BEF��B����ת����Ƕȣ���ͼ����ʾ����������Ӧ���߶Σ��ʣ�1���еĽ����Ƿ���Ȼ������ͨ���۲��㻹�ܵó�ʲô���ۣ�����Ҫ��֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�������ȷ���ǣ� ��
A��2x+3y =5xy B��x��x4=x4 C��x8��x2=x4 D����x2y��3=x6y3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com