
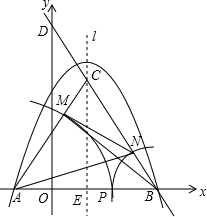 ��ͼ��ʾ��������y=-x2+2x+8��x�ύ��A��B���㣬ֱ��BD�Ľ���ʽΪy=-2$\sqrt{3}x$+8$\sqrt{3}$�������ߵĶԳ���l��ֱ��BD���ڵ�C����x�ύ�ڵ�E��
��ͼ��ʾ��������y=-x2+2x+8��x�ύ��A��B���㣬ֱ��BD�Ľ���ʽΪy=-2$\sqrt{3}x$+8$\sqrt{3}$�������ߵĶԳ���l��ֱ��BD���ڵ�C����x�ύ�ڵ�E������ ��1�������ߵĽ���ʽ�У���y=0���������A��B������ꣻ���������ߵĶԳ��᷽�̼�ֱ��BD�Ľ���ʽ�������C������ꣻ
��2���ٸ��ݵ������ε����ʣ�������ȣ��ɵ�AM=BN������Բ�����ʣ��ɵ�AM��AP��BN��BP�Ĺ�ϵ�������߶��е�����ʣ��ɵô𰸣�
����ͼ֪���ı���AMNB�����Ϊ��ABC���CMN�������ȱߡ�ABC���������ã��ؼ������CMN���������M��MF��CN��F����AP=AM=m�������m��ʾ��CM��BN��CN�ij�����������Rt��MFC�У����ݡ�ACB������ֵ���MF�ı���ʽ���ɴ˿ɵõ���CMN�������������ù����ı���AMNB�������m�ĺ�����ϵʽ�����ɸ��ݺ�������������ı���AMNB��������Сֵ��
��� �⣺��1����-x2+2x+8=0��
��ã�x1=-2��x2=4��
��A��-2��0����B��4��0��
��y=-x2+2x+3=-��x-1��2+4��
�������ߵĶԳ���Ϊx=1��
��x=1����y=-2$\sqrt{3}x$+8$\sqrt{3}$��
��y=6$\sqrt{3}$��
��C��1��6$\sqrt{3}$����
��2���ٴ���һ��P��ʹ���ı���AMNBΪ�������Σ�
���ı���AMNBΪ�������Σ���
AM=BN=AP=BP��
��P��AB���е㣬A��-2��0����B��4��0����
AP=BP=$\frac{3-��-1��}{2}$=2��
-1+2=1��
��P��1��0����
���ı���AMNB���������Сֵ��
��AP=m���ı���AMNB�����ΪS��
�ɹ��ɶ�������
AC=$\sqrt{A{C}^{2}+C{E}^{2}}$=$\sqrt{{2}^{2}+��6\sqrt{3}��^{2}}$=6
��AB=BC�TAB=4��BN=CM=BP=4-m��
S��ABC=$\frac{\sqrt{3}}{4}$��62=9$\sqrt{3}$��
��CM=BN=BP=6-m��CN=m��
��ͼ��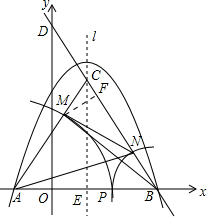 ��
��
��M��MF��BC������ΪF
��MF=MC•sin60��=$\frac{\sqrt{3}}{2}$��6-m����
��S��CMN=$\frac{1}{2}$CN•MF=$\frac{1}{2}$m•$\frac{\sqrt{3}}{2}$��6-m��=-$\frac{\sqrt{3}}{4}$m2+$\frac{3\sqrt{3}}{2}$m��
��S=S��ABC-S��CMN
=9$\sqrt{3}$-��-$\frac{\sqrt{3}}{4}$m2+$\frac{3\sqrt{3}}{2}$m��
=$\frac{\sqrt{3}}{4}$��m-2��2+$\frac{27\sqrt{3}}{4}$��
��m=2ʱ��Sȡ����Сֵ$\frac{27\sqrt{3}}{4}$��
���� ���⿼���˶��κ����ۺ��⣬�����˶��κ���ͼ���������ύ����������ȱ������ε����ʣ��������εĶ��壬��������ĺͲ���������������Ĺؼ���


 ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�AD��BC��AD=3��BC=9��AB=6��CD=4����EF��BC��������AEFD������EBCF���ܳ���ȣ���EF�ij�Ϊ$\frac{39}{5}$��
��ͼ��������ABCD�У�AD��BC��AD=3��BC=9��AB=6��CD=4����EF��BC��������AEFD������EBCF���ܳ���ȣ���EF�ij�Ϊ$\frac{39}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
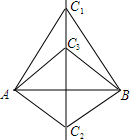 ��֪����ͼ��C1A=C1B��C2A=C2B��C3��ֱ��C1C2��һ�㣮��֤��C3A=C3B��
��֪����ͼ��C1A=C1B��C2A=C2B��C3��ֱ��C1C2��һ�㣮��֤��C3A=C3B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
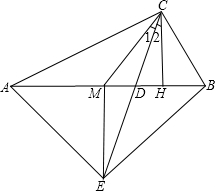 ��֪����ͼ����Rt��ABC�У���ACB=90�㣬��M��AB�ߵ��е㣬CH��AB�ڵ�H��CDƽ�֡�ACB��
��֪����ͼ����Rt��ABC�У���ACB=90�㣬��M��AB�ߵ��е㣬CH��AB�ڵ�H��CDƽ�֡�ACB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com