
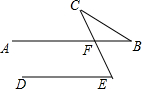
 如图,AB∥DE,∠E=60°,则∠B+∠C=60°.
如图,AB∥DE,∠E=60°,则∠B+∠C=60°.  53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
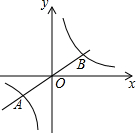 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
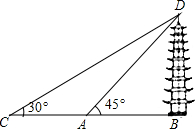 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
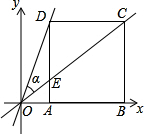 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
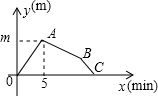 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com