
如图,已知抛物线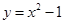 与
与 轴交于A、B两点,与
轴交于A、B两点,与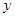 轴交于点C.
轴交于点C.
【小题1】求A、B、C三点的坐标.
【小题2】过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
【小题3】在 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG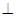
 轴于点G,使以A、M、G三点为顶点的三角形与
轴于点G,使以A、M、G三点为顶点的三角形与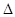 PCA相似.若存在,直接写出所有满足要求的M点的坐标;否则,请说明理由.
PCA相似.若存在,直接写出所有满足要求的M点的坐标;否则,请说明理由.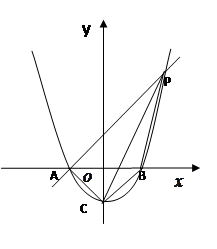
【小题1】令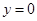 ,得
,得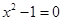 解得
解得
令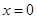 ,得
,得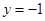
∴ A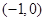 B
B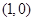 C
C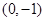 ..................................3分
..................................3分
【小题1】∵OA=OB=OC= ∴
∴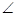 BAC=
BAC=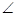 ACO=
ACO=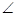 BCO=
BCO=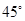
∵AP∥CB, ∴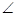 PAB=
PAB=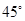
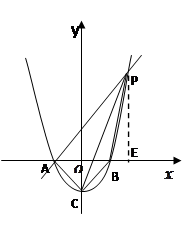
过点P作PE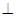
 轴于E,则
轴于E,则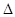 APE为等腰直角三角形
APE为等腰直角三角形
令OE=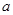 ,则PE=
,则PE=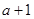 ∴P
∴P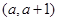
∵点P在抛物线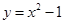 上 ∴
上 ∴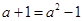
解得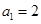 ,
,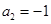 (不合题意,舍去)
(不合题意,舍去)
∴PE=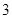
∴四边形ACBP的面积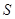 =
= AB•OC+
AB•OC+ AB•PE=
AB•PE=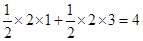
【小题1】满足要求的M点有三个,(-2,0)、(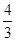 ,0)、(4,0).
,0)、(4,0).
解析【小题1】抛物线与x轴的交点,即当y=0,C点坐标即当x=0,分别令y以及x为0求出A,B,C坐标的值;
【小题1】四边形ACBP的面积=△ABC+△ABP,由A,B,C三点的坐标,可知△ABC是直角三角形,且AC=BC,则可求出△ABC的面积,根据已知可求出P点坐标,可知AP的长度,以及点B到直线的距离,从而求出△ABP的面积,则就求出四边形ACBP的面积;
【小题1】假设存在这样的点M,两个三角形相似,根据题意以及上两题可知,∠PAC∠和∠MGA是直角,只需证明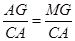 或
或 即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
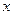 轴交于点
轴交于点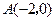 ,
,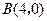 ,与
,与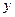 轴交于点
轴交于点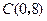 .
.
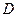 的坐标;
的坐标;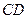 交
交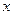 轴于点
轴于点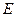 .在线段
.在线段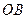 的垂直平分线上是否存在点
的垂直平分线上是否存在点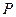 ,使得点
,使得点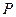 到直线
到直线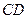 的距离等于点
的距离等于点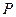 到原点
到原点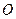 的距离?如果存在,求出点
的距离?如果存在,求出点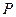 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;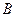 作
作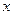 轴的垂线,交直线
轴的垂线,交直线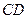 于点
于点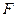 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段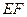 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?查看答案和解析>>
科目:初中数学 来源: 题型:
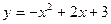 与
与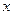 轴的两个交点为A、B,与
轴的两个交点为A、B,与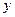 轴交于点C
轴交于点C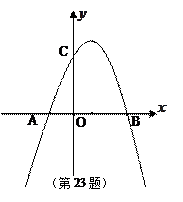
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与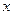 轴交于点
轴交于点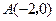 ,
,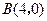 ,与y轴交于点
,与y轴交于点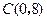 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交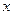 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与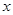 轴交于点
轴交于点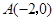 ,
,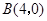 ,与y轴交于点
,与y轴交于点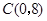 .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交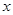 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,已知抛物线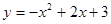 与
与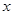 轴的两个交点为A、B,与
轴的两个交点为A、B,与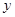 轴交于点C
轴交于点C
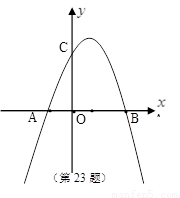
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com