
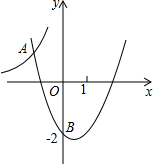 如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-
如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-| 8 |
| x |
| A、y=x2-x-2 |
| B、y=x2-x+2 |
| C、y=x2+x-2 |
| D、y=x2+x+2 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=| 4 |
| 5 |
| 25 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、6厘米 | B、12厘米 |
| C、24厘米 | D、36厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=| 1 |
| 2 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:| 等级 | 成绩(S) | 频数 |
| A | 90<S≤100 | x |
| B | 80<S≤90 | 15 |
| C | 70<S≤80 | 10 |
| D | S≤70 | 3 |
| 合计 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
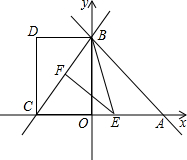 如图,在平面直角坐标系xoy中,直线y=-
如图,在平面直角坐标系xoy中,直线y=-| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com