
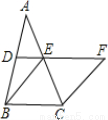
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明见解析;(2) .
.
【解析】
试题分析:从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为4,求出菱形的高面积就可求.
试题解析:(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=FE,
∴四边形BCFE是菱形;
(2)【解析】
∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
,
∴菱形的面积为4× =
= .
.
考点:1.菱形的判定与性质;2.三角形中位线定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届湖南长沙麓山国际实验学校八年级下学期期中数学试卷(解析版) 题型:选择题
如图是香港特别行政区的区徽,区徽中的紫荆花图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°

查看答案和解析>>
科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:选择题
甲、乙两人赛跑,所跑路程与时间的关系如图(实线为甲的路程与时间的关系图象,虚线为乙的路程与时间的关系图象),小王根据图象得到如下四条信息,其中错误的是( )

A.这是一次1500m赛跑
B.甲、乙同时起跑
C.甲、乙两人中先到达终点的是乙
D.甲在这次赛跑中的速度为5m/s
查看答案和解析>>
科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点P(﹣3,4)关于x轴的对称点的坐标是( )
A.(﹣4,﹣3) B.(﹣3,﹣4) C.(3, 4) D.(3,﹣4)
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:解答题
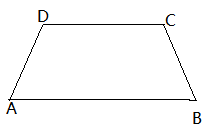
如图,(1)在梯形ABCD中,AB∥DC,若∠A=∠B,求证:AD=BC
(2)写出(1)的逆命题,并证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com