
 在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=
在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA= .则下列关系式中不成立的是
.则下列关系式中不成立的是
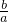 =1,关系式成立;
=1,关系式成立; ,tanA•cosA=
,tanA•cosA=
 =
= ,关系式成立;
,关系式成立; ,cotA•sinA=
,cotA•sinA= •
• =
= ,关系式成立;
,关系式成立; )2+(
)2+( )2≠1,关系式不成立.
)2≠1,关系式不成立. 或sinA=tanA•cosA.
或sinA=tanA•cosA.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com