解:由图1得,AB=AE+BF,由图2得,AB=BF-AE,由图3得AB=AE-BF.
证明:如图1,延长AC交BF于M,
∵l
1∥l
2,
∴∠2=∠AMB,
在△ABC和△MBC中

∴△ABC≌△MBC(ASA)
∴AC=CM,AB=MB.
在△AEC和△CFM中

,
∴△AEC≌△CFM(ASA)
∴AE=MF
∵BM=MF+BF.
∴AM=AE+BF.
如图2,AB=BF-AE
延长AC交BF于M,
∵l
1∥l
2,
∴∠AEC=∠AFM,
在△ABC和△MBC中

∴△ABC≌△MBC(ASA)
∴AC=CM,AB=MB.
在△AEC和△CFM中

,
∴△AEC≌△CFM(ASA)
∴AE=MF
∵BM=BF-MF,
∴AB=BF-AE
如图3,AB=AE-BF.
延长AC交BF于M,
∵l
1∥l
2,

∴∠2=∠AMB,
在△ABC和△MBC中

∴△ABC≌△MBC(ASA)
∴AC=CM,AB=MB.
在△AEC和△CFM中

,
∴△AEC≌△CFM(ASA)
∴AE=MF.
∵BM=MF-BF,
∴AB=AE-MF.
分析:延长AC交BF于M,分别证明△ABC≌△MBC就可以得出AC=MC,再证明△AEC≌△MFC就看得出结论,由图1、图2、图3就有三个不同的结论.
点评:本题考查了平行线的性质的运用,全等三角形的判定及性质的运用,解答时正确作辅助线是解答的关键.



 ,
,
 ,
,

 ,
,

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案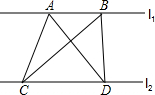 如图,l1∥l2,A、B为直线l1上两点,C、D为直线l2上两点,则△ACD与△BCD的面积大小关系是( )
如图,l1∥l2,A、B为直线l1上两点,C、D为直线l2上两点,则△ACD与△BCD的面积大小关系是( )