

分析 (1)根据4级的天数数除以4级所占的百分比,可得答案;
(2)根据圆周角乘以3级所占的百分比,可得答案;
(3)根据有理数的减法,可得5级的天数,根据5级的天数,再根据样本数据估计总体,可得答案.
解答 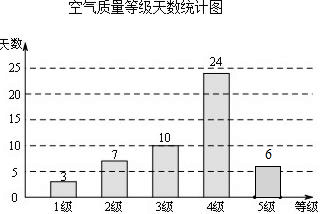 解:(1)本次调查共抽取了24÷48%=50(天),
解:(1)本次调查共抽取了24÷48%=50(天),
故答案为:50;
(2)360°×$\frac{10}{50}$=72°,
故答案为:72;
(3)5级抽取的天数50-3-7-10-24=6天,
365×$\frac{24+6}{50}$×100%=219(天),
答:2015年该城市有219天不适宜开展户外活动.
点评 本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

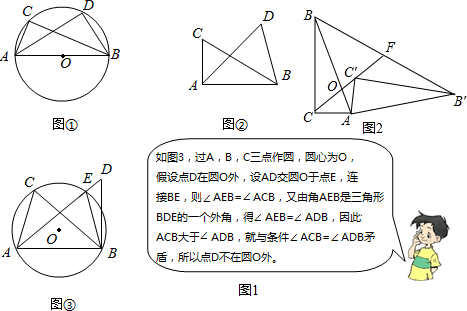
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
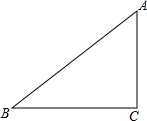 如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com