
| A. | $\frac{21}{16}$ | B. | $\frac{63}{16}$ | C. | -$\frac{21}{16}$ | D. | -$\frac{63}{16}$ |
分析 先解方程$\frac{x+1}{2}-\frac{2x-1}{5}$=0,得x=-7,根据两个方程的解相同,把得x=-7代入方程x+$\frac{6a-x}{2}=\frac{a}{3}$,可得关于a的一元一次方程,解方程即可.
解答 解:解方程$\frac{x+1}{2}-\frac{2x-1}{5}$=0,得x=-7.
把x=-7代入方程x+$\frac{6a-x}{2}=\frac{a}{3}$,得
-7+$\frac{6a+7}{2}$=$\frac{a}{3}$,
解得a=$\frac{21}{16}$.
故选A.
点评 本题考查了解一元一次方程,利用了同解方程的定义得出关于a的一元一次方程是解题关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
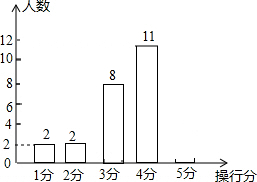 某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人 数 | 2 | 4 | 10 | 30 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
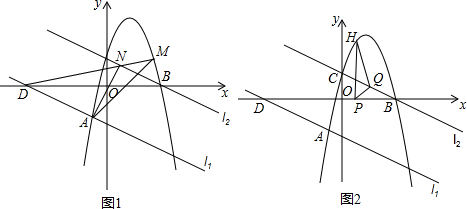
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是实数,且|a|≥0 | B. | $\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程 | ||
| C. | 三角形内角和等于360° | D. | a是实数,a0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
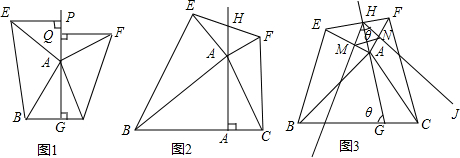
 如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
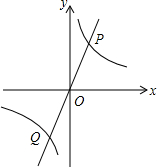 如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.
如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com