解:(1)结论仍然成立.理由为:
连接AP,延长PE交AD于点M,
∵△ABC、△ADE均为等腰直角三角形,
∴∠BAC=∠DAE=45°,∴∠DAB=90°,
∵P为BD中点,∴PA=PB=PD,
在△APC和△BPC中,
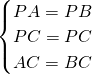
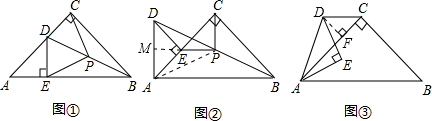
,
∴△APC≌△BPC(SSS),
∴∠ACP=∠BCP=

∠ACB=45°,
同理可得△APE≌△DPE,
∴∠APE=∠DPE,∠PAE=∠PDE,
∴∠APE+∠PAE=∠DPE+∠PDE,即∠AEM=∠DEM=

∠AED=45°,
∴∠CEP=∠AEM=45°,
∴∠CPE=90°,
∴△CPE为等腰直角三角形,即PC=PE,PC⊥PE;
(2)过D作DF⊥AC,垂足为F,
∵DC∥AB,∴∠DCF=∠CAB=45°,
∴DF=CF,
在Rt△ADF中,∠DAF=30°,
设DF=k,则有AD=2k,AF=

k,
∴AC=AF+FC=

k+k=(

+1)k,
∴

=
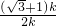
=

.
分析:(1)结论仍成立,理由如下:在图②上连接AP,延长PE与AD交于点M,由三角形ABC与三角形ADE都为等腰直角三角形,根据等腰三角形的性质可得∠CAB与∠DAE都为45°,进而得到∠DAB为直角,又P为斜边BD的中点,AP为斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半,可得DP=BP=AP,再由AC=BC,且CP为公共边,利用SSS可证明三角形ACP与三角形BCP全等,可得∠ACP=∠BCP,从而得到∠ECP=45°,同理可得三角形DPE与三角形APE全等,可得∠DEP=∠AEP,即∠CEP=∠AEM=45°,可得三角形EPC为等腰直角三角形,得证;
(2)过D作DF垂直于AC,垂足为F,由三角形ABC为等腰三角形且DC与AB平行,根据等腰三角形的性质及两直线平行内错角相等可得∠DCF=45°,可得三角形DCF为等腰直角三角形,得到DF=CF,在直角三角形ADF中,设30°角所对的直角边DF=k,斜边AD=2k,根据勾股定理求得AF=

k,由AF+FC表示出AC,即可求出AC与AD的比值.
点评:此题考查了等腰三角形的判定与性质,全等三角形的判定与性质,平行线的性质以及直角三角形的性质,其中第二、三问根据题意及分析作出合适的辅助线是解题的关键.

 的值.
的值.
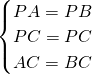 ,
, ∠ACB=45°,
∠ACB=45°, ∠AED=45°,
∠AED=45°,
 k,
k, k+k=(
k+k=( +1)k,
+1)k, =
=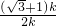 =
= .
. k,由AF+FC表示出AC,即可求出AC与AD的比值.
k,由AF+FC表示出AC,即可求出AC与AD的比值.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案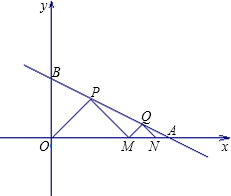 ∠OPM=∠MQN=90°.试求:
∠OPM=∠MQN=90°.试求: