
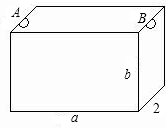
 如图,为处理含有某种杂质同的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a,b乘积ab成反比,现有制箱材料60平方米,问当a,b各为
如图,为处理含有某种杂质同的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a,b乘积ab成反比,现有制箱材料60平方米,问当a,b各为| k |
| ab |
| ab |
| k |
| ab |
| 30-a |
| 2+a |
| k |
| ab |
| k | ||
|
| k | ||
-a+32-
|
| k | ||
34-(a+2+
|
| k | ||||
34-2
|
| k |
| 18 |
| 64 |
| a+2 |
| 2ab |
| 2 |
| ab |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com