
【题目】如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.

【答案】(1)图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∠1+∠A=90°,
∠2=∠A,
∠1=∠B.
【解析】试题分析:(1)由题中已知条件∠ACB=90°,CD是高,可以得到∠ADC、∠BDC、∠ACB都是直角。
(2)由(1)得到ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,所以∠1+∠A=90°,∠1+∠2=90°∠B+∠A=90°,由此可以得到∠2=∠A,∠1=∠B。
试题解析:(1) ![]() ∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∠1+∠A=90°,∠2=∠A,∠1=∠B.
![]() ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B
ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B


科目:初中数学 来源: 题型:
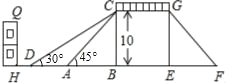
【题目】如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明(在括号中填写推理理由) 如图,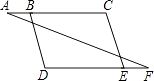
已知∠A=∠F,∠C=∠D,求证:BD∥CE.
证明:因为∠A=∠F,
所以AC∥DF(),
所以∠C+∠=180°().
因为∠C=∠D,
所以∠D+∠=180°(),
所以BD∥CE().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,AD∥BC,∠DAC=120°. 
(1)若AB平分∠DAC,求∠ABC的度数.
(2)若∠ACF=20°,求∠BCF的度数.
(3)在(2)的条件下,若CE平分∠BCF,求∠CEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1) 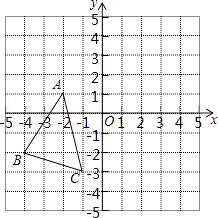
(1)A′、B′两点的坐标分别为A′、B′;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com