Question

如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E．

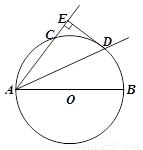
（1）判断直线DE与⊙O的位置关系，并说明理由；

（2）若AE＝8，⊙O的半径为5，求DE的长．

 

Answer 1

【答案】

（1）相切；（2）4

【解析】

试题分析：（1）连接OD，根据角平分线的性质可得∠EAD＝∠OAD，根据圆的基本性质可得∠ODA＝EAD，即可证得EA∥OD，再结合DE⊥AC即可证得结论；

（2）作DF⊥AB，垂足为F，先证得△EAD≌△FAD，根据全等三角形的性质可得AF＝AE＝8，DF＝DE，再在Rt△DOF中，根据勾股定理求得DF的长，即可求得结果.

（1）直线DE与⊙O相切．

连接OD．

∵AD平分∠BAC，

∴∠EAD＝∠OAD．

∵OA＝OD，

∴∠ODA＝∠OAD．

∴∠ODA＝EAD．

∴EA∥OD． 

∵DE⊥EA，

∴DE⊥OD．

又∵点D在⊙O上，

∴直线DE与⊙O相切；

（2）作DF⊥AB，垂足为F．

∴∠DFA＝∠DEA＝90°．

∵∠EAD＝∠FAD，AD＝AD，

∴△EAD≌△FAD．

∴AF＝AE＝8，DF＝DE．

∵OA＝OD＝5，

∴OF＝3．

在Rt△DOF中，DF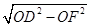＝＝4．

∴DE＝DF＝4．

考点：角平分线的性质，圆的基本性质，切线的判定，全等三角形的判定和性质，勾股定理

点评：本题知识点较多，是小综合题，在中考中比较常见，一般难度不大.