
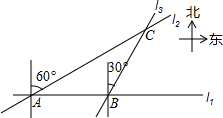
 如图,A、B、C是三座城市,A市在B市的正西方向.C市在A市北偏东60°的方向,在B市北偏东30°的方向.这三座城市之间有高速公路l1、l2、l3相互贯通.小亮驾车从A市出发,以平均每小时80公里的速度沿高速公路l2向C市驶去,3小时后小亮到达了C市.
如图,A、B、C是三座城市,A市在B市的正西方向.C市在A市北偏东60°的方向,在B市北偏东30°的方向.这三座城市之间有高速公路l1、l2、l3相互贯通.小亮驾车从A市出发,以平均每小时80公里的速度沿高速公路l2向C市驶去,3小时后小亮到达了C市. )
)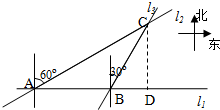 (1)解:过点C作CD⊥l1于点D,由已知得 …
(1)解:过点C作CD⊥l1于点D,由已知得 … AC=
AC= ×240=120(km)…
×240=120(km)…
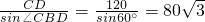 …
…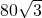 …
…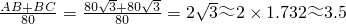 …
…

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明)
如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com