
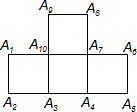
 如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成多少个等腰直角三角形?你愿意把得到上述结论的探究方法与他人交流吗?若愿意,请简要写出你的探究过程.
如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成多少个等腰直角三角形?你愿意把得到上述结论的探究方法与他人交流吗?若愿意,请简要写出你的探究过程.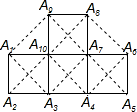 解:如图,①等腰直角三角形有:△A1A2A3,△A1A2A10,△A2A2A10,△A1A3A10,
解:如图,①等腰直角三角形有:△A1A2A3,△A1A2A10,△A2A2A10,△A1A3A10,

科目:初中数学 来源:2011年浙江省温州市初中毕业生学业仿真考试数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com