
分析 (1)延长AP交CD于点Q,则可得到∠BAP=∠AQC,则∠APC=∠BAP+∠DCP=2(∠MAP+∠MCP),连接MP并延长到点R,则可得∠APR=∠MAP+∠AMP,∠CPR=∠MCP+∠CMP,可得到∠P和∠M的关系,从而求解;
(2)如图2,过P作PQ∥AB于Q,MN∥AB于N,则AB∥PQ∥MN∥CD,根据平行线的性质得到∠APQ=180°-∠BAP,∠CPQ=180°-∠DCP,∠AMN=∠BAM,∠CMN=∠DCM,根据角平分线的定义得到∠BAP=2∠BAM,∠DCP=2∠DCM,等量代换即可得到结论;
(3)如图3,过P作PQ∥AB于Q,MN∥AB于N,则AB∥PQ∥MN∥CD,设∠MCD=x,则∠PCM=2x,∠PCD=3x,设∠PAM=y,则∠MAB=y,则∠PAB=2y,根据平行线的性质得到∠QPA=∠PAB=2y,∠NMA=∠MAB=y,列方程即可得到结论.
解答 解:(1)如图1,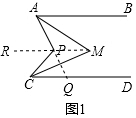 延长AP交CD于点Q,则可得到∠BAP=∠AQC,
延长AP交CD于点Q,则可得到∠BAP=∠AQC,
则∠APC=∠BAP+∠DCP=2(∠MAP+∠MCP),
连接MP并延长到点R,则可得∠APR=∠MAP+∠AMP,∠CPR=∠MCP+∠CMP,
所以∠APC=∠M+∠MAP+∠MCP,
所以∠APC=∠M+$\frac{1}{2}$∠APC,
所以∠M=$\frac{1}{2}$∠APC=55°.
故答案为:55;
(2)如图2,过P作PQ∥AB于Q,MN∥AB于N,
则AB∥PQ∥MN∥CD,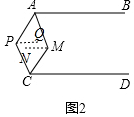
∴∠APQ=180°-∠BAP,∠CPQ=180°-∠DCP,∠AMN=∠BAM,∠CMN=∠DCM,
∵AM平分∠BAP,CM平分∠PCD,
∴∠BAP=2∠BAM,∠DCP=2∠DCM,
∴∠APC=∠APQ+∠CPQ=180°-∠BAP+180°-∠DCP=360°-2(∠BAM+∠DCM)=360°-2(∠BAM+∠DCM)=360°-2∠AMC;
(3)如图3,过P作PQ∥AB于Q,MN∥AB于N,
则AB∥PQ∥MN∥CD,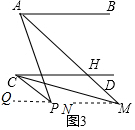
设∠MCD=x,则∠PCM=2x,∠PCD=3x,设∠PAM=y,则∠MAB=y,则∠PAB=2y,
∵AB∥PQ,
∴∠QPA=∠PAB=2y,∠NMA=∠MAB=y,
∴∠QPA=∠CPQ+∠CPA=∠PCD+∠CPA=3x+∠CPA ①,∠NMA=∠NMC+∠AMC=∠MCD+∠AMC=x+∠AMC ②,
∵2∠AMC-∠APC=10°,2∠AMC=2(∠NMA-∠NMC)=2(y-x),∠APC=∠APQ-∠CPQ=2y-3x,
∴2(y-x)-(2y-3x)=10°,
∴x=10°,
∴∠PCD=3x=30°.
点评 本题主要考查外角的性质及角平分线的定义、平行线的性质,解题的关键是利用三角形的外角的性质找到∠P和∠M之间的关系.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com