
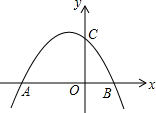
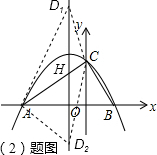
 (2013•苍梧县一模)如图,抛物线y=-
(2013•苍梧县一模)如图,抛物线y=-| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |
|
|
| 3 |
| 4 |
-
| ||
2×(-
|
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 27 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
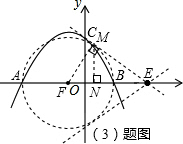
| EF2-FM2 |
| 52-32 |
| MN |
| ME |
| FN |
| FM |
| FM |
| EF |
| MN |
| 4 |
| FN |
| 3 |
| 3 |
| 5 |
| 12 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
 (2013•苍梧县一模)某闭合电路中,电源的电压为定值,电流强度I(A)与电阻R(Ω)成反比例关系,其函数图象如图所示,则电流强度I(A)与电阻R(Ω)的函数解析式是
(2013•苍梧县一模)某闭合电路中,电源的电压为定值,电流强度I(A)与电阻R(Ω)成反比例关系,其函数图象如图所示,则电流强度I(A)与电阻R(Ω)的函数解析式是| 6 |
| R |
| 6 |
| R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com