
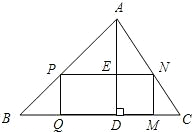
 下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.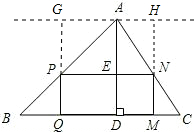 解:(1)设长方形零件PQMN的边PN=a,PQ=x,则AE=80-x.
解:(1)设长方形零件PQMN的边PN=a,PQ=x,则AE=80-x. .
.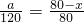 .
. x.
x. x)=-
x)=- x2+120x.
x2+120x. =40时,a=60.
=40时,a=60. ×120×80-2×2400=0,
×120×80-2×2400=0, AD=40,故P,Q分别为AB,AC的中点,易证△PBQ≌△PAG,△NMC≌△NHA,可达到拼接的目的.
AD=40,故P,Q分别为AB,AC的中点,易证△PBQ≌△PAG,△NMC≌△NHA,可达到拼接的目的.

科目:初中数学 来源: 题型:
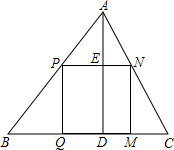 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是查看答案和解析>>
科目:初中数学 来源: 题型:
 19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)
19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为
如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为查看答案和解析>>
科目:初中数学 来源: 题型:
 19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.
19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com