练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知一次函数y=kx+b，当x=2时，y=5；当x=-2时，y=-11，求k和b的值．

    分析 将已知两对x与y的值代入一次函数解析式即可求出k与b的值．

    解答 解：将x=2，y=5；x=-2，y=-11分别代入一次函数解析式得：
    $\left\{\begin{array}{l}{5=2k+b}\\{\;}\\{-11=-2k+b}\end{array}\right.$，
    解得：k=4，b=-3．

    点评 此题主要考查了待定系数法求一次函数解析式，利用二元一次方程组是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

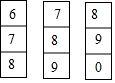    2．如图是鹏鹏存钱罐的密码锁（每个密码都是0-9中的一个数），该密码锁的一个密码是7，后两位的密码鹏鹏记不清了，他只记得后两位的密码都比6大，则鹏鹏第一次就能打开改密码锁的概率是（　　）
    A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{1}{8}$D．$\frac{1}{9}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

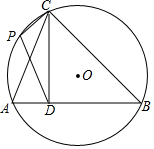    3．△ABC内接于圆O，CD⊥AB于D，CD=DB=3，AD=1，点P为$\widehat{AC}$上一点，求$\frac{\sqrt{10}}{2}$DP+CP的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：（$\frac{1}{2}$）-1-（-1）2017-（π-3）0+$\sqrt{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，把△ABC绕着点A顺时针方向旋转32°，得到△AB'C'，恰好B'，C，C'三点在一直线上，则么∠C'=74°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，矩形ABCD中，E是边BC的一点，F是边CD的中点，CE=k•BE，且四边形AECF的面积为2．
    （1）当k=1时，求AB•BE的值；
    （2）用含k的代数式表示△ABE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知x-y=6，xy=-8．
    （1）求x2+y2的值；
    （2）求x4+y4的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

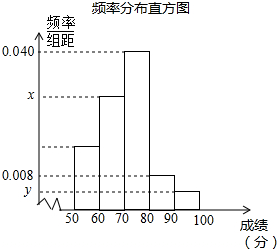    1．为参加学校的“我爱古诗词”知识竞赛，小王所在班级组织了一次古诗词知识测试，并将全班同学的分数（得分取正整数，满分为100分）进行统计，以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图．
    组别分组频数频率
    1　50≤x＜6090.18
    2　60≤x＜70a
    3　70≤x＜80200.40
    4　80≤x＜900.08
    5　90≤x≤1002b
    合计
    请根据以上频率分布表和频率分布直方图，回答下列问题：
    （1）求出a、b、x、y的值；
    （2）若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛，请用“列表法”或“树状图”求出小明、小敏同时被选中的概率．（注：五位同学请用A、B、C、D、E表示，其中小明为A，小敏为B）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

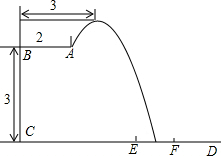    2．2016年里约奥运会，中国跳水队赢得8个项目中的7块金牌，优秀成绩的取得离不开艰辛的训练．某跳水运动员在进行跳水训练时，身体（看成一点）在空中的运动路线是如图所示的一条抛物线，已知跳板AB长为2米，跳板距水面CD的高BC为3米，训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米，现以CD为横轴，CB为纵轴建立直角坐标系．
    （1）当k=4时，求这条抛物线的解析式；
    （2）当k=4时，求运动员落水点与点C的距离；
    （3）图中CE=$\frac{19}{4}$米，CF=$\frac{21}{4}$米，若跳水运动员在区域EF内（含点E，F）入水时才能达到训练要求，求k的取值范围．

    查看答案和解析>>

    同步练习册答案