
分析 (1)原式仿照阅读材料中的方法:结果与分母只差一个符号,根据此规律求出值即可;
(2)原式第一个括号中仿照阅读材料中的方法变形,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$(n为正整数);
(2)原式=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}-\sqrt{3}$)+…+($\sqrt{2017}-\sqrt{2016}$),
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2017}-\sqrt{2016}$,
=$\sqrt{2017}$-1.
点评 此题考查了分母有理化,弄清阅读材料中的方法是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 包场计费:包场每场每小时50元,每人须另付入场费5元 |
| 人数计费:每人打球2小时20元,接着续打球每人每小时6元 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8元或10元 | B. | 12元 | C. | 8元 | D. | 10元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
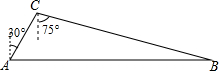 如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.
如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com