
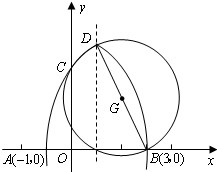
解:(1)设抛物线的解析式为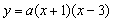 则 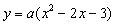 =a(x-1)2-4a =a(x-1)2-4a则点D的坐标为  点C的坐标为 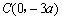 。 。 |
|
| (2)过点D作DE⊥y轴于E,如图①所示: 则有△DEC∽△COB ∴ 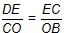 ∴  ∴a2=1,a=±1 抛物线的解析式为y=x2-2x-3或y=-x2+2x+3。 |
 |
| (3)a<0时,a=-1,抛物线y=-x2+2x+3, 这时可以找到点Q,很明显,点C即在抛物线上, 又在⊙G上,∠BCD=90°,这时Q与C点重合,点Q坐标为Q(0,3) 如图②,若∠DBQ为90°,作QF⊥y轴于F,DH⊥x轴于H 可证Rt△DHB∽Rt△BFQ 有  则点Q坐标(k,-k2+2k+3) 即 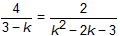 化简为2k2-3k-9=0 即(k-3)(2k+3)=0 解之为k=3或k= 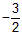 由k= 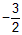 得Q坐标: 得Q坐标: |
 |
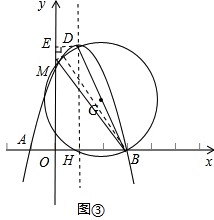
| 如图③,延长DQ交y轴于M,作DE⊥y轴于E,DH⊥x轴于H 可证明△DEM∽△DHB 即 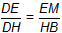 则 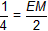 得 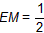 点M的坐标为  DM所在的直线方程为 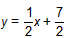 则 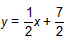 与y=-x2+2x+3的解为 与y=-x2+2x+3的解为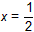 得交点坐标Q为 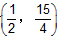 即满足题意的Q点有三个:(0,3), 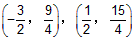 。 。 |
 |


科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 3 |
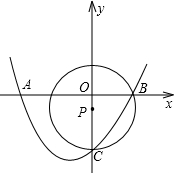 并说明理由;
并说明理由;查看答案和解析>>
科目:初中数学 来源: 题型:
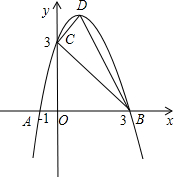 正半轴于点C,设抛物线的顶点为D.
正半轴于点C,设抛物线的顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com