⊙O的半径为1,以O为原点建立直角坐标系,正方形ABCD的顶点B的坐标为(5,0),点D在⊙O上运动,当CD与圆相切时,直线OD的解析式为________.
y=-
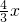
或y=-

x
分析:分两种情况:①D
1点在第二象限时;②D
2点在第四象限时;再根据相似三角形的性质,可得比例关系式,代入数据可得CD所在直线对应的函数关系.
解答:
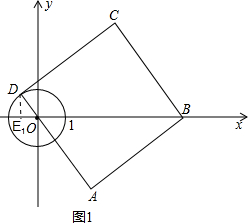
解:直线CD与⊙O相切分两种情况:
①如图1,设D
1点在第二象限时,
过D
1作D
1E
1⊥x轴于点E
1,设此时的正方形的边长为a,
∴(a-1)
2+a
2=5
2,
∴a=4或a=-3(舍去),
∵Rt△BOA∽Rt△D
1OE
1
∴
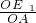
=
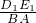
=
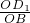
,
∴OE
1=

,D
1E
1=

,
∴D
1(-

,

),
代入y=kx,

=-

k,
∴k=-

,
∴直线OD的函数关系式为y=-

x,
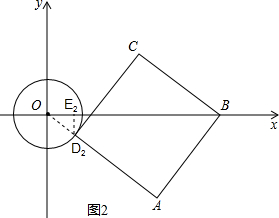
②如图2,设D
2点在第四象限时,过D
2作D
2E
2⊥x轴于点E
2,
设此时的正方形的边长为b,则(b+1)
2+b
2=5
2,
解得b=3或b=-4(舍去).
∵Rt△BOA∽Rt△D
2OE
2,
∴
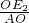
=
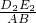
=
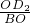
,
∴OE
2=

,D
2E
2=

,
∴D
2(

,-

),
代入y=ax,
-

=

a,
∴k=-

,
∴直线OD的函数关系式为y=-

x,
故答案为:y=-
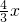
或y=-

x.
点评:此题主要考查了一次函数的综合应用,本题难度较大,要求学生有较强的综合分析能力及数形结合分析解决问题的能力.

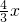 或y=-
或y=- x
x 解:直线CD与⊙O相切分两种情况:
解:直线CD与⊙O相切分两种情况: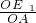 =
=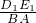 =
=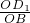 ,
, ,D1E1=
,D1E1= ,
, ,
, ),
), =-
=- k,
k, ,
, x,
x,
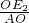 =
=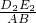 =
=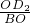 ,
, ,D2E2=
,D2E2= ,
, ,-
,- ),
), =
= a,
a, ,
, x,
x,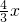 或y=-
或y=- x.
x.

 已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-
已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-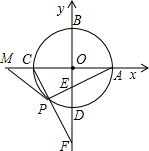 如图,以⊙O两条互相垂直的直径所在直线为轴建立平面直角坐标系,两坐标轴交⊙O于A,B,C,D四点,点P在弧CD上,连PA交y轴于点E,连CP并延长交y轴于点F.
如图,以⊙O两条互相垂直的直径所在直线为轴建立平面直角坐标系,两坐标轴交⊙O于A,B,C,D四点,点P在弧CD上,连PA交y轴于点E,连CP并延长交y轴于点F.