解:(1)E(-4,-

),F(

,3);
(2)结论EF∥AB.理由如下:
∵P(-4,3),
∴E(-4,-

),F(

,3),
即得PE=3+

,PF=

+4,
在Rt△PAB中,tan∠PAB=
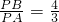
,
在Rt△PEF中,tan∠PEF=
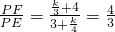
,
∴tan∠PAB=tan∠PEF,
∴∠PAB=∠PEF,
∴EF∥AB;
(3)S有最小值.理由如下:
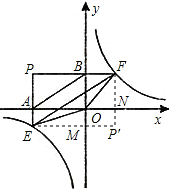
分别过点E、F作PF、PE的平行线,交点为P′.
由(2)知P′(
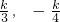
)
∵四边形PEP′F是矩形,
∴S
△P′EF=S
△PEF,
∴S=S
△PEF-S
△OEF=S
△P′EF-S
△OEF=S
△OME+S
矩形OMP′N+S
△ONF=
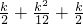
=
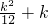
=
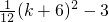
,
又∵k≥2,此时S的值随k值增大而增大,
∴当k=2时,S
最小=

.
∴S的最小值是

.
故答案为:(1)(-4,-

),(

,3).
分析:(1)把x=-4,y=3分别代入y=

,求出对应的y值与x值,从而得出点E、点F的坐标;
(2)根据三角函数的定义,在Rt△PAB中与Rt△PEF中,分别求出tan∠PAB与tan∠PEF的值,然后由平行线的判定定理,得出EF与AB的位置关系;
(3)如果分别过点E、F作PF、PE的平行线,交点为P′,则四边形PEP′F是矩形.所求面积S=S
△PEF-S
△OEF=S
△P′EF-S
△OEF=S
△OME+S
矩形OMP′N+S
△ONF,根据反比例函数比例系数k的几何意义,可用含k的代数式表示S,然后根据二次函数的性质及自变量的取值范围确定S的最小值.
点评:本题主要考查了三角函数的定义,平行线的判定,反比例函数比例系数的几何意义及二次函数最小值的求法等知识点,综合性较强,难度较大.

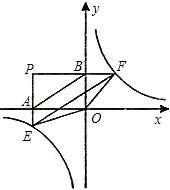 如图,过点P(-4,3)作x轴,y轴的垂线,分别交x轴,y轴于A、B两点,交双曲线y=
如图,过点P(-4,3)作x轴,y轴的垂线,分别交x轴,y轴于A、B两点,交双曲线y= (k≥2)于E、F两点.
(k≥2)于E、F两点. ),F(
),F( ,3);
,3); ),F(
),F( ,3),
,3), ,PF=
,PF= +4,
+4,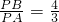 ,
,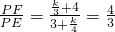 ,
,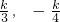 )
)
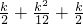
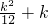
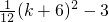 ,
, .
. .
. ),(
),( ,3).
,3). ,求出对应的y值与x值,从而得出点E、点F的坐标;
,求出对应的y值与x值,从而得出点E、点F的坐标;

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案 8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
 如图,过点O、A(1,0)、B(0,
如图,过点O、A(1,0)、B(0, 如图,过点P(2,
如图,过点P(2, 如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例y=
如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例y=