
 �Ķ�������ϣ�����ѧ���ϣ���ʦ����������⣺
�Ķ�������ϣ�����ѧ���ϣ���ʦ����������⣺���� ֱ�������߶δ�ֱƽ���ߵ������Լ�ֱ�ߵ����ʽ��������ó��𰸣�
��� �⣺�ֱ��Ե�A�͵�BΪԲ�ģ�����$\frac{1}{2}$AB�ij�Ϊ�뾶�����������ཻ��C��D����������ǣ����߶������˵������ȵĵ����߶εĴ�ֱƽ�����ϣ�
����CD�������ǣ�����ȷ��һ��ֱ�ߣ�
�ʴ�Ϊ�����߶������˵������ȵĵ����߶εĴ�ֱƽ�����ϣ�����ȷ��һ��ֱ�ߣ�
���� ������Ҫ�����˻�����ͼ���߶δ�ֱƽ���ߵ����ʣ���ȷ������������ǽ���ؼ���


 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��A��B�Ƿ���������y=$\frac{k}{x}$��k��0�������㣬AC��x�ᣬBD��y�ᣬ��S��ADE��S��BCE�Ĺ�ϵ��Σ�
��ͼ��A��B�Ƿ���������y=$\frac{k}{x}$��k��0�������㣬AC��x�ᣬBD��y�ᣬ��S��ADE��S��BCE�Ĺ�ϵ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪�����ε���������x���ϣ�������������������y=3-x2�ϣ�����������ε������
��֪�����ε���������x���ϣ�������������������y=3-x2�ϣ�����������ε�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
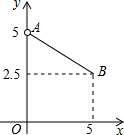 ��ͼ�Ǻ���y=$\frac{1}{2}$x+5��һ����ͼ������ͼ��ش��������⣺
��ͼ�Ǻ���y=$\frac{1}{2}$x+5��һ����ͼ������ͼ��ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com