
| 3 |

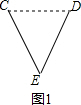 解:(1)连接CD(图1).
解:(1)连接CD(图1).| CH |
| CE |
| ||
| 2 |
| 3 |
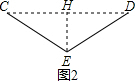
| 3 |
| 3 |
| 3 |
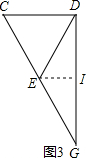
| DI |
| DE |
| ||
| 2 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
| A、一组邻边相等的矩形是正方形 |
| B、有一个角是直角的平行四边形是正方形 |
| C、对角线互相垂直的矩形是正方形 |
| D、对角线相等的菱形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
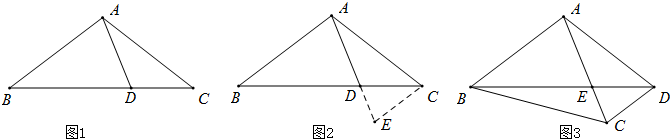
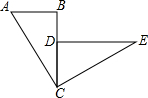 如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是
如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是查看答案和解析>>
科目:初中数学 来源: 题型:
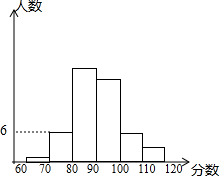 第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
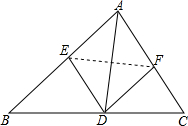 如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.
如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com