
 (2008•鄂尔多斯)在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题:
(2008•鄂尔多斯)在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题: ;y乙=______;
;y乙=______; ;
; ≈4.7,
≈4.7,

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
 (2008•鄂尔多斯)在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题:
(2008•鄂尔多斯)在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题: ;y乙=______;
;y乙=______;查看答案和解析>>
科目:初中数学 来源:2008年内蒙古鄂尔多斯市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年内蒙古鄂尔多斯市中考数学试卷(解析版) 题型:选择题
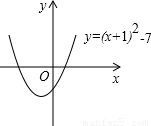
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com