
 ,另再送50元现金(注:每次购买电器时只能使用其中一种优惠方式)
,另再送50元现金(注:每次购买电器时只能使用其中一种优惠方式) x+50;
x+50; x+50.
x+50. n+100=800,
n+100=800, m+
m+ n=800,解得m+n=3200,3200-50×2=3100元.
n=800,解得m+n=3200,3200-50×2=3100元. x+50,(x≥600),依此求解.
x+50,(x≥600),依此求解. =优惠劵金额求出②
=优惠劵金额求出②

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:解答题
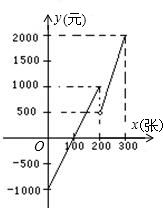 某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.
某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
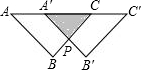 如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为________cm.
如图,将两个边长为2cm且互相重合的正方形纸片沿对角线翻折成等腰直角三角形后,再抽出一个等腰直角三角形沿AC边移动,若重叠部分面积为1cm2,则它移动的距离AA′为________cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
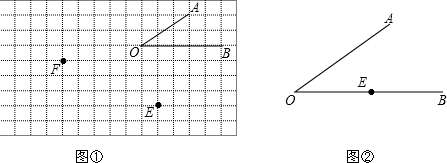
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com