
【题目】正方形![]() 的边长为1,点
的边长为1,点![]() 是
是![]() 边上的一个动点(与
边上的一个动点(与![]() ,
,![]() 不重合),以
不重合),以![]() 为顶点在
为顶点在![]() 所在直线的上方作
所在直线的上方作![]()
(1)当![]() 经过点
经过点![]() 时,
时,
①请直接填空:![]() ________(可能,不可能)过
________(可能,不可能)过![]() 点:(图1仅供分析)
点:(图1仅供分析)
②如图2,在![]() 上截取
上截取![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,作
,作![]() 于
于![]() ,求证:四边形
,求证:四边形![]() 为正方形;
为正方形;
③如图2,将②中的已知与结论互换,即在![]() 上取点
上取点![]() (
(![]() 点在正方形
点在正方形![]() 外部),过
外部),过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,作
,作![]() 于
于![]() ,若四边形
,若四边形![]() 为正方形,那么
为正方形,那么![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)当点![]() 在射线
在射线![]() 上且
上且![]() 不过点
不过点![]() 时,设
时,设![]() 交边
交边![]() 于
于![]() ,且
,且![]() .在
.在![]() 上存在点
上存在点![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,使得
,使得![]() ,连接
,连接![]() ,则当
,则当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?



【答案】(1)①不可能 ②详见解析处 ③结论:OA=OE,理由:详见解析处 (2)当BO为![]() 时,四边形PKBG的面积最大,最大值
时,四边形PKBG的面积最大,最大值![]() .
.
【解析】
(1)①若ON过点D,则在△OAD中不能满足勾股定理,据此可知ON不可能过点D;
②由条件可判断出四边形EFCH为矩形,再证明△OFE≌△ABO,可得结论;
③结论:OA=OE,如图2-1中,连接EC,在BA上取一点Q,使得BQ=BO,连接OQ,证明△AQO≌△OCE即可.
(2)根据条件可证明△PKO∽△OBG,利用相似三角形的性质可得OP=1,可得△POG面积为定值及△PKO和△OBG的关系,只要△OGB的面积有最大值时,四边形PKBG的面积也最大,设OB=a,BG=b,由勾股定理可用b表示出a,则可用a表示出△OBG的面积,利用二次函数的性质即可求得其最大值,继而可求得四边形PKBG的面积最大值.
解:(1)①若ON过点D,则OA>AB,OD>CD,
∴OA2>AD2,OD2>AD2,
∴OA2 +OD2>2AD2≠AD2,
∴∠AOD≠90°,这与∠MON=90°矛盾,
∴ON不可能过点D,
故答案为:不可能;
②如图2中,
∵EH⊥CD,EF⊥BC,
∴∠EHC=∠EFC=90°且∠HCF=90°,
∴四边形EFCH为矩形,
∵∠MON=90°,
∴∠EOF=90°-∠AOB,
在正方形ABCD中,
∠BAO=90°-∠AOB,
∴∠EOF=∠BAO,
在△OFE和△ABO中,  ,
,
∴△OFE≌△ABO(AAS)
∴EF=OB,OF=AB,
又∵OF=CF+OC=AB=BC=BO+OC=EF+OC,
∴CF=EF,
∴四边形EFCH为正方形;
③结论:OA=OE
理由:如图2-1所示,连接EC,在BA上取一点Q,使得BQ=BO,连接OQ.

∵AB=BC,BQ=BO,
∴AQ=OC
∵∠QAO=∠EOC,∠AQO=∠ECO=135°,
∴△AQO=△OCE(ASA)
∴OA=EO
(2)
∵∠POK=∠OGB,∠PKO=∠OBG,
∴△PKO∽△OBG,
∵S△PKO=![]() S△OBG,
S△OBG,
∴ ,
,
∴OP=1,
∴S△POG=![]() ·OG·OP=/span>
·OG·OP=/span>![]() ×1×2=1,
×1×2=1,
设OB=a,BG=b,则a2+b2=OG2=4,
∴b=![]() ,
,
∴S△OBG=![]() ab=
ab=![]() a
a![]() =
=![]()
![]() =
=![]()
![]() ,
,
∴当a2=2时,S△OBG有最大值1,此时S△PKO=![]() S△OBG=
S△OBG=![]() ,
,
∴四边形PKBG的最大面积为1+1+![]() =
=![]()
∴当BO为![]() 时,四边形PKBG的面积最大,最大值
时,四边形PKBG的面积最大,最大值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(1)求直线![]() 和该抛物线的解析式;
和该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的上方,过点
的上方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,直线
之间的一个动点,直线![]() 、
、![]() 与
与![]() 分别交于
分别交于![]() 、
、![]() ,当点
,当点![]() 运动时,求
运动时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能写成![]() 的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
(1)请证明:28和217都是婆罗摩笈多数。
(2)请证明:任何两个婆罗摩笈多数的乘积依旧是婆罗摩笈多数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠xOy=90°,线段AB=10,若点A在Oy上滑动,点B随着线段AB在射线Ox上滑动(A,B与O不重合),Rt△AOB的内切圆☉K分别与OA,OB,AB切于点E,F,P.
(1)在上述变化过程中,Rt△AOB的周长,☉K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由.
(2)当AE=4时,求☉K的半径r.
(3)当Rt△AOB的面积为S,AE为x,试求S与x之间的函数关系,并求出S最大时直角边OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB![]() AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF
AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF![]() ∠A,另一边EF交AC于点F.
∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当D为AB中点时,四边形ADEF的形状为 (直接写出结论);
(3)延长图1中的DE到点G,使EG![]() DE,连接AE,AG,FG,得到图2.若AD
DE,连接AE,AG,FG,得到图2.若AD![]() AG,判断四边形AEGF的形状,并说明理由.
AG,判断四边形AEGF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民夏季(5月—10月)阶梯电价价目如右表.李叔叔家8月份用电500度,他家这个月要电费___元.张阿姨家8月份缴纳电费249.4元,她家这个月用电___度.(不计公共分摊部分).
阶梯 | 电量(度) | 电价/度 |
第一档 | 0—260部分 | 0.59元 |
第二档 | 261—600部分 | 0.64元 |
第三档 | 601度以上部分 | 0.89元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
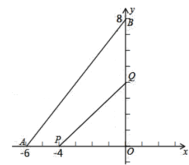
【题目】已知:如图所示,在△ABO中,∠AOB=90°,AO=6cm,BO=8cm,AB=10cm.且两直角边落在平面直角坐标系的坐标轴上.
(1)如果点P从A点开始向O以1cm/s的速度移动,点Q从点O开始向B以2cm/s的速度移动.P,Q分别从A,O同时出发,那么几秒后,△POQ为等腰三角形?
(2)若M,N分别从A,O出发在三角形的边上运动,若M点运动的速度是xcm/s,N点运动的速度是ycm/s,当M,N相向运动时,2s后相遇,当M,N都沿着边逆时针运动时9s后相遇.求M、N的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com